| (9.4) |
separando le variabili ed in forma sinusoidale. La forma del disturbo
Si può ovviamente immaginare come esistano circostanze limite al di sotto delle quali le perturbazioni risultano smorzate, ed al di sopra delle quali risultano amplificate. Il numero di Reynolds rappresenta quindi un parametro certamente discriminante nell'instaurarsi del regime turbolento, poiché come detto in 9.2.1 esso rappresenta il rapporto tra le forze d'inerzia e viscose che regolano il moto.
In generale interessa studiare il caso tridimensionale di nascita e sviluppo delle piccole perturbazioni ma, tenendo conto del teorema di Squire secondo il quale i disturbi bidimensionali sono sempre più instabili di quelli tridimensionali, lo studio del caso bidimensionale fornirebbe certamente una soluzione conservativa, oltre che più facilmente perseguibile. Le principali esemplificazioni introdotte saranno:
| (9.4) |
![$\displaystyle \hat{u}\ =\ \ensuremath{\frac{\partial \psi}{\partial y}}\ =\ \ensuremath{\frac{\partial \phi}{\partial y}} \exp{[i \alpha(x - ct)]}
$](img1065.png)
mentre secondo
![$\displaystyle \hat{v}\ =\ -\ensuremath{\frac{\partial \psi}{\partial x}}\ =\ -i \alpha\ \phi\ \exp{[i \alpha(x - ct)]}
$](img1067.png)
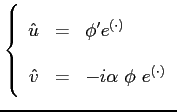 |
(9.5) |
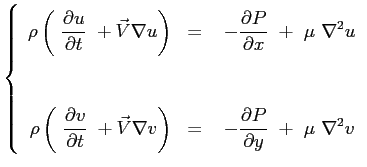 |
(9.6) |
![\begin{displaymath}
\begin{array}{rcl}
\displaystyle \ensuremath{\frac{\partial ...
...rtial^2 \hat{v}}{\partial y^2}} \right)\\ [3pt] \\
\end{array}\end{displaymath}](img1071.png)
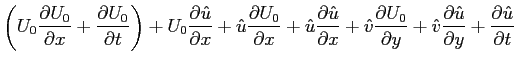 |
|||
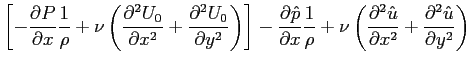 |
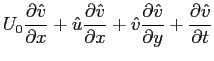 |
|||
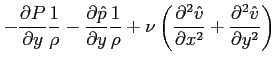 |
![$\displaystyle \left( U_0\ensuremath{\frac{\partial U_0}{\partial x}} + \ensurem...
...{\partial x^2}}+\ensuremath{\frac{\partial^2 U_0}{\partial y^2}}\right)\right]
$](img1076.png)
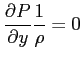
rappresentano l'equazione di Navier-Stokes alla componente media del flusso, quindi automaticamente soddisfatti. Il termine
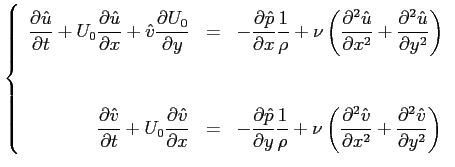 |
(9.7) |
![\begin{displaymath}
\left\{
\begin{array}{rcl}
-i \alpha c \phi' e^{(\cdot)} + U...
...)} - i \alpha \phi^{''} e^{(\cdot)} \right]
\end{array}\right.
\end{displaymath}](img1086.png)
Svolgendo i calcoli:
![\begin{displaymath}
\left\{
\begin{array}{rcl}
-i \alpha c \phi' e^{(\cdot)} + U...
...)} - i \alpha \phi^{''} e^{(\cdot)} \right]
\end{array}\right.
\end{displaymath}](img1086.png)
e derivando la prima rispetto a
![\begin{displaymath}
\left\{
\begin{array}{rcr}
-i \alpha c \phi^{''} e^{(\cdot)}...
...a \phi^{''} (i \alpha) e^{(\cdot)}\right]&&
\end{array}\right.
\end{displaymath}](img1087.png)
semplificando, sottraendo la seconda equazione dalla prima e dividendo per
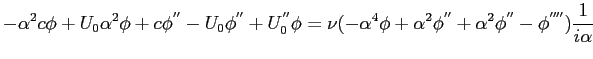
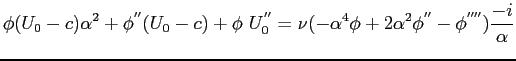
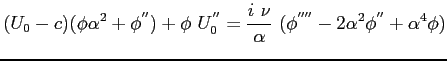
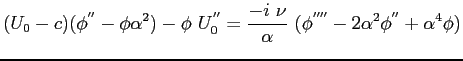 |
(9.8) |
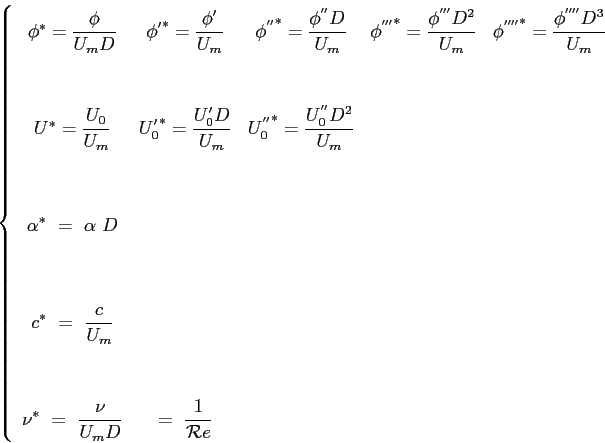
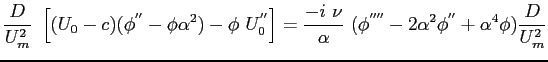
La Eq. 9.9 rappresenta l'equazione di Orr-Sommerfeld. ![]() e
e ![]() rappresentano rispettivamente la velocità massima nel flusso e una dimensione caratteristica del flusso medio (ad esempio la larghezza del condotto) oppure dello strato limite (ad esempio lo spessore dello strato limite).
Essa non è di facile soluzione soprattutto nel caso di profilo
rappresentano rispettivamente la velocità massima nel flusso e una dimensione caratteristica del flusso medio (ad esempio la larghezza del condotto) oppure dello strato limite (ad esempio lo spessore dello strato limite).
Essa non è di facile soluzione soprattutto nel caso di profilo ![]() generico. Per una soluzione numerica della Eq. 9.9 si veda ad esempio [8] o anche [9].
generico. Per una soluzione numerica della Eq. 9.9 si veda ad esempio [8] o anche [9].
Lin (1945) usò a tale proposito la via della teoria asintotica, mentre Wazzan (1968) percorse la strada della soluzione numerica diretta. Schubauer e Skramstad (1947) procedettero ponendo dei nastri metallici magnetici sottili nello strato limite laminare di una piastra piana. Eccitarono questi nastri facendoli vibrare al fine di produrre dei disturbi di lunghezza d'onda nota. L'accordo tra i dati teorici e sperimentali è mostrato in figura Fig. 9.2. Si può notare come ad un dato valore del
![]() basato sullo spessore di spostamento, corrispondano un valore minimo e massimo del parametro
basato sullo spessore di spostamento, corrispondano un valore minimo e massimo del parametro
![]() delimitanti una zona instabile di amplificazione delle perturbazioni.
delimitanti una zona instabile di amplificazione delle perturbazioni.
![\includegraphics[width=130mm]{dito.eps}](img1100.png)
|
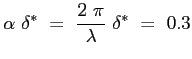
riprendendo i dati della soluzione esatta di Blasius di Tab. 7.1:
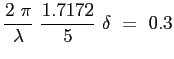
Queste onde prendono il nome di onde di Tollmein-Schlichting dal nome dei ricercatori che contribuirono allo sviluppo della teoria.
Sfortunatamente però l'insorgere della instabilità del flusso non coincide necessariamente con la transizione.