



Next: Richiami sui vettori
Up: Transizione da moto laminare
Previous: Teoria idrodinamica della stabilità
Indice
È un metodo euristico di predizione della transizione sviluppato da Jaffe nel 1970. Si basa sull'idea razionale, seppur non totalmente rigorosa secondo la quale esiste un punto di stabilità neutro al di sopra del quale l'amplificazione dei disturbi cresce rapidamente: l'instaurarsi di piccoli disturbi bidimensionali porta alla nascita di disturbi tridimensionali e successivamente allo sviluppo del regime turbolento. Il metodo 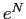 , operante su disturbi bidimensionali, valuta l'evoluzione dell'amplificazione del disturbo nel flusso lungo la superficie, a valle del punto di stabilità neutra, integrandolo e cercando di ottenere un valore universale per
, operante su disturbi bidimensionali, valuta l'evoluzione dell'amplificazione del disturbo nel flusso lungo la superficie, a valle del punto di stabilità neutra, integrandolo e cercando di ottenere un valore universale per 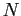 che indichi la transizione. Bisognerà dapprima analizzare l'andamento spaziale dei piccoli disturbi, piuttosto che quello temporale. I due saranno identici solo nel caso di stabilità neutra. Il parametro
che indichi la transizione. Bisognerà dapprima analizzare l'andamento spaziale dei piccoli disturbi, piuttosto che quello temporale. I due saranno identici solo nel caso di stabilità neutra. Il parametro 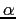 sarà un numero complesso la cui parte immaginaria
sarà un numero complesso la cui parte immaginaria 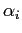 rappresenta il fattore di amplificazione.
rappresenta il fattore di amplificazione.
Il procedimento di attuazione del metodo procede attraverso passi successivi:
- per un dato campo di velocità esterno allo strato limite, per assegnate condizioni al contorno e numero di Reynolds, si determina il profilo di velocità (e la sua derivata seconda) nello strato limite stesso e si risolverà successivamente l'equazione Eq. 9.9 di Orr-Sommerfeld ottenendo una mappa delimitante la zona di stabilità analoga alla Fig. 9.2;
- il secondo passo consisterà nella generazione di un profilo di velocità laminare il più accurato possibile in varie stazioni lungo la superficie di contatto
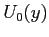 , dal punto di arresto fino a ben oltre la stazione di calcolo dove ci si aspetta la transizione. Il calcolo di stabilità verrà fatto partire da un valore del
, dal punto di arresto fino a ben oltre la stazione di calcolo dove ci si aspetta la transizione. Il calcolo di stabilità verrà fatto partire da un valore del
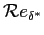 leggermente più grande del
leggermente più grande del
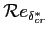 su un punto del ramo inferiore della curva a dito di Fig. 9.2 corrispondente ad una certa coordinata
su un punto del ramo inferiore della curva a dito di Fig. 9.2 corrispondente ad una certa coordinata 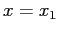 . Ripetendo il calcolo per punti successivi con frequenze differenti9.2 si perverrà al diagramma di Fig. 9.3.;
. Ripetendo il calcolo per punti successivi con frequenze differenti9.2 si perverrà al diagramma di Fig. 9.3.;
- il terzo passo consisterà nell'implementare il metodo, vedere se i risultati teorici concordano con quelli sperimentali e portano ad un valore universale del fattore di amplificazione che può essere adottato come criterio per la predizione della transizione.
Il numero 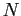 tiene conto del rapporto, ad una data frequenza, tra l'ampiezza del disturbo ad una data ascissa oltre il punto neutro, e l'ampiezza nel punto neutro stesso di stabilità :
tiene conto del rapporto, ad una data frequenza, tra l'ampiezza del disturbo ad una data ascissa oltre il punto neutro, e l'ampiezza nel punto neutro stesso di stabilità :
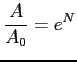 |
(9.10) |
in cui:
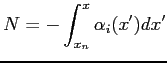 |
(9.11) |
Figura 9.3:
Lastra piana: Andamento dell'amplificazione alle varie frequenze di disturbo. (Da Jaffe, 1970)
|
|
Un ampio confronto tra risultati numerici e sperimentali su corpi di varia forma ha portato ad assumere un valore medio:
tuttavia recentemente si tende a preferire un approccio differente secondo il quale si cerca piuttosto di determinare il valore di 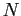 che permette di avere un riscontro positivo con i dati sperimentali.
che permette di avere un riscontro positivo con i dati sperimentali.




Next: Richiami sui vettori
Up: Transizione da moto laminare
Previous: Teoria idrodinamica della stabilità
Indice
2009-01-26
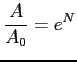
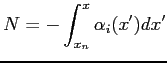
![\includegraphics[width=100mm]{transition.eps}](img1111.png)