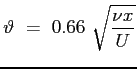Next: Teoria idrodinamica della stabilità
Up: Transizione da moto laminare
Previous: Il numero di Reynolds
Indice
Il criterio di Michel (1952) è un criterio molto semplice sulla predizione della transizione basato sul numero di Reynolds riferito allo spessore di quantità di moto e sul numero di Reynolds locale nel punto in cui avviene la transizione:
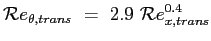 |
(9.3) |
La relazione 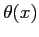 può essere ottenuta per esempio dalla Eq. 6.17 di Thwaites. Si valuta il legame tra
può essere ottenuta per esempio dalla Eq. 6.17 di Thwaites. Si valuta il legame tra
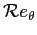 e
e
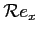 e quindi il valore di
e quindi il valore di
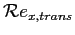 dalla relazione di Michel.
dalla relazione di Michel.
Nel caso della lastra piana si può utilizzare la soluzione esatta di Blasius 7.5:
e quindi ottenere:
Sostituendo nella relazione di Michel:
e risolvendo numericamente:
I risultati del criterio di Michel sono affidabili al
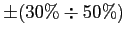 .
.
2009-01-26