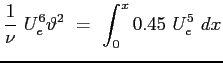Next: Equazione di Blasius: soluzione
Up: Risoluzione integrale delle equazioni
Previous: Parametri di strato limite
Indice
Il metodo integrale di Thwaites è basato sull'equazione di Von Kàrmàn e sull'assunzione di valori numerici empirici che trovano riscontro nella realtà.
È in molti casi un metodo molto accurato. Dato il campo esterno 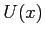 si vogliono determinare
si vogliono determinare
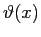 ,
,
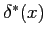 e
e 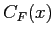 . Si riprenda l'Eq. (6.5):
. Si riprenda l'Eq. (6.5):
Volendo integrarla per ottenere l'andamento dello spessore di quantità di moto 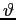 la si riscrive:
la si riscrive:
Si dovrà cercare di mettere in relazione il fattore di forma 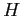 e il coefficiente di attrito a parete
e il coefficiente di attrito a parete 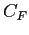 con
con 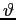 . L'adimensionalizzazione di
. L'adimensionalizzazione di 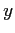 avverrà ora tenendo in considerazione lo spessore di quantità di moto
avverrà ora tenendo in considerazione lo spessore di quantità di moto 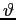 :
:
mentre la velocità adimensionata resterà :
Il profilo di velocità nello strato limite è caratterizzato da:
-
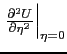 curvatura del profilo a parete, legata alla derivata della velocità esterna
curvatura del profilo a parete, legata alla derivata della velocità esterna
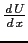 .
.
La curvatura (cambiata di segno) a parete viene chiamata:
Parametro di Thwaites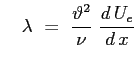 |
(6.14) |
-
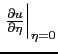 pendenza del profilo a parete, legata al coefficiente d'attrito
pendenza del profilo a parete, legata al coefficiente d'attrito 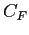 :
:
La pendenza del profilo di velocità a parete sarà rappresentata dal parametro 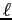 :
:
Thwaites assunse che i parametri 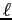 e
e 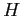 fossero unicamente funzioni di
fossero unicamente funzioni di 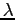 parametro di Thwaites:
parametro di Thwaites:
Relazioni usate per il calcolo di 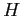 e
e 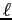 , una volta ottenuto
, una volta ottenuto 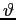 e quindi
e quindi 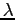 sono quelle di Cebecy & Bradshaw:
sono quelle di Cebecy & Bradshaw:
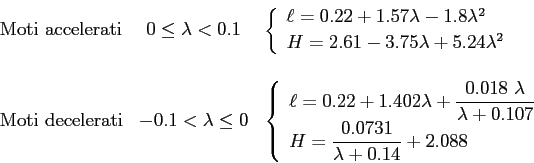 |
|
|
(6.15) |
Si moltiplichi per
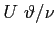 l'equazione di Von Kàrmàn:
l'equazione di Von Kàrmàn:
A questo punto entra in gioco una ulteriore assunzione, empirica, di Thwaites basata su riscontri sperimentali:
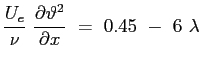 |
(6.16) |
Con l'espressione di 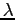 :
:
e moltiplicando per 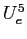 :
:
Questa equazione può essere facilmente integrata:
Al punto di arresto, 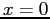 è
è 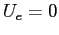 :
:
In definitiva lo spessore di quantità di moto risulta:
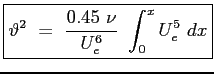 |
(6.17) |
Una volta noto
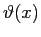 è possibile ottenere
è possibile ottenere
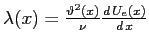 ,
, 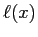 ed
ed 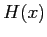 dalle (6.15), e finalmente lo spessore di spostamento
dalle (6.15), e finalmente lo spessore di spostamento
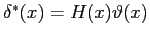 che permette di ricalcolare il campo di moto esterno, e il coefficiente di attrito
che permette di ricalcolare il campo di moto esterno, e il coefficiente di attrito
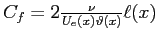 . Osservando l'andamento dello sforzo a parete
. Osservando l'andamento dello sforzo a parete 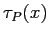 si cercherà di determinare il punto di separazione.
si cercherà di determinare il punto di separazione.
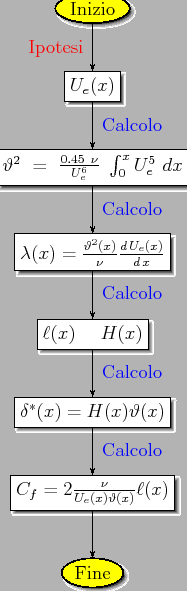
Tabella 6.5:
Utilizzo del metodo di Thwaites.
 |




Next: Equazione di Blasius: soluzione
Up: Risoluzione integrale delle equazioni
Previous: Parametri di strato limite
Indice
2009-01-26
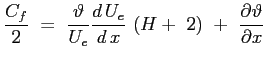
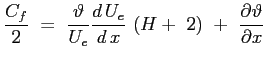
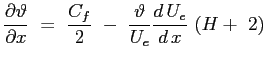
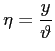
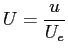
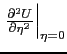 curvatura del profilo a parete, legata alla derivata della velocità esterna
curvatura del profilo a parete, legata alla derivata della velocità esterna
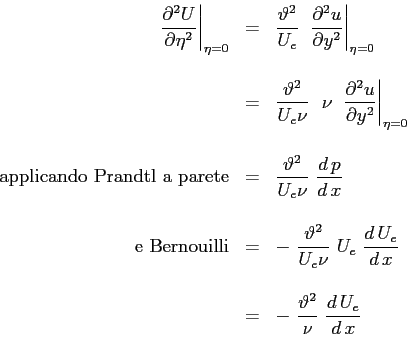
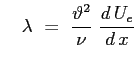
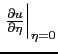 pendenza del profilo a parete, legata al coefficiente d'attrito
pendenza del profilo a parete, legata al coefficiente d'attrito 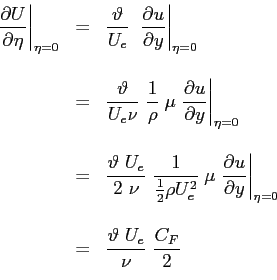
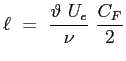
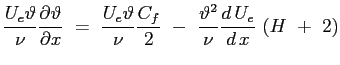
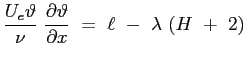
![$\displaystyle \frac{U_e}{\nu} \ \ensuremath{\frac{\partial \vartheta^2}{\partial x}} \ = \ 2 \ [\ell \ -\ \lambda \ (H \ +\ 2)]
$](img650.png)
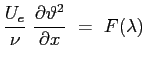
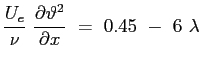
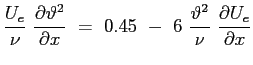
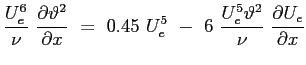
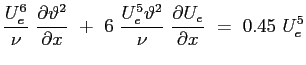
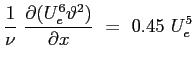
![$\displaystyle \left[\frac{1}{\nu}\ U_e^6\vartheta^2\right]^x_0 \ =\ \int_0^x{0.45 \ U_e^5 \ dx}
$](img658.png)