



Next: Soluzione
Up: Atti di moto laminare
Previous: Soluzione
Indice
La condizione di aderenza richiede che su qualsiasi punto della superficie di un solido immerso in un campo di moto, la velocità sia nulla. Per punto di arresto si intende quel punto paticolare della superficie in cui la linea di corrente incidente è perpendicolare alla superficie stessa. Nel punto di arresto la velocità locale è nulla sia in presenza di fluido ideale che viscoso. Pur potendo essere curva ma non angolosa, la superficie in un intorno del punto di arresto, può essere in prima approssimazione essere ritenuta piana.
Figura 8.3:
Campo di moto in prossimità del punto di arresto.
|
|
Il campo di moto irrotazionale esterno allo strato limite, nell'intorno del punto di arresto, può essere ragionevolmente ipotizzato di tipo iperbolico con una funzione di corrente del tipo:
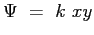 |
(8.4) |
con 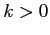 e:
e:
All'interno dello strato limite:
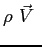
grad
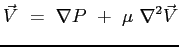
Figura 8.4:
Andamento del campo di velocità
|
|
Si noti come l'equazione, in forma vettoriale non introduca le semplificazioni di Prandtl. Si assume l'assenza di forze di volume e la bidimensionalità del campo di moto, discendente dall'ipotesi fatta sulla funzione di corrente. Al fine di procedere alla ricerca di una soluzione del campo di moto all'interno dello strato limite si applica l'operatore rotore all'equazione appena scritta così da far sparire il termine dipendente dalla pressione (dipendente a sua volta sia da 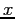 che da
che da 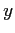 ):
):
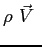
grad
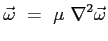
La vorticità
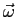 è un vettore perpendicolare al piano del moto, essendo il campo di moto bidimensionale, per cui si potrà scrivere:
è un vettore perpendicolare al piano del moto, essendo il campo di moto bidimensionale, per cui si potrà scrivere:
in cui il tensore del secondo ordine
grad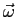 è diventa in effetti un vettore. Ci si è così ricondotti ad una unica equazione scalare:
è diventa in effetti un vettore. Ci si è così ricondotti ad una unica equazione scalare:
Si deve ora introdurre una ulteriore ipotesi, questa volta relativa ad un plausibile campo di moto interno allo strato limite8.2. Si ipotizzerà che la funzione di corrente, all'interno dello strato limite, continui ad essere dipendente linearmente da 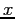 ma dipendente da
ma dipendente da 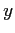 secondo una funzione incognita. In questo modo si ipotizza che l'influenza dello strato limite sulla funzione di corrente dipenda solo dalla vicinanza al contorno solido:
secondo una funzione incognita. In questo modo si ipotizza che l'influenza dello strato limite sulla funzione di corrente dipenda solo dalla vicinanza al contorno solido:
Con questa funzione di corrente si ottiene:
si può scrivere:
Integrando con le condizioni al contorno:
c.c.
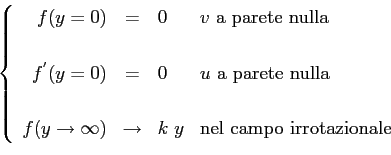
e sostituendo:
si ottiene:
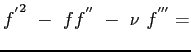
cost
e finalmente sfruttando le c.c.:
Si può procedere ulteriormnte col l'adimensionalizzazione introducendo le variabili:
Si arriva in definitiva alla:
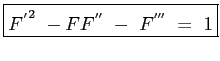 |
(8.5) |
con le condizioni al contorno:
c.c.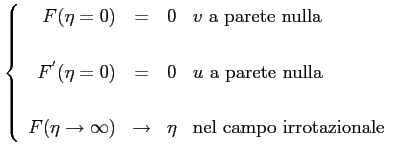 |
(8.6) |
Si vede che la Eq. (8.5) ha la forma della Eq. (8.1) con 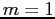 . In quest'ultima tuttavia
. In quest'ultima tuttavia 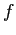 esprime la funzione di corrente adimensionata, mentre nel caso in studio
esprime la funzione di corrente adimensionata, mentre nel caso in studio 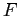 esprime la componente
esprime la componente 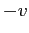 della velocità adimensionata; inoltre anche l'ultima delle condizioni al contorno è differente.
della velocità adimensionata; inoltre anche l'ultima delle condizioni al contorno è differente.
Subsections




Next: Soluzione
Up: Atti di moto laminare
Previous: Soluzione
Indice
2009-01-26
![\includegraphics[width=75mm]{punto_arresto.eps}](img911.png)
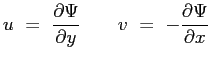
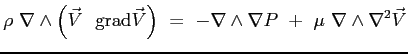
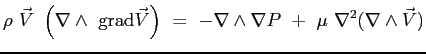
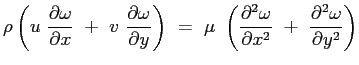
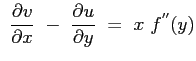
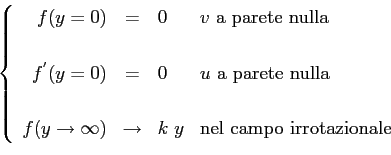
![\begin{displaymath}
\begin{array}{rcl}
\int{f^{'}f^{''} dy} \ &=& \ f^{'}f^{'} -...
...=& \ ff^{''} - \ \frac{1}{2} \ {f^{'}}^2\\ [3pt]\\
\end{array}\end{displaymath}](img935.png)
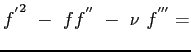 cost
cost
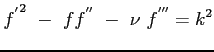
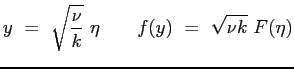
![\begin{displaymath}
\begin{array}{rcl}
f^{'} \ &=& \displaystyle \ \sqrt{\nu k}\...
... \displaystyle \frac{k^2}{\nu} \ F^{'''}\\ [3pt]\\
\end{array}\end{displaymath}](img939.png)