Strato limite Falkner-Skan

Le equazioni di Prandtl vengono risolte introducendo l'ipotesi che il moto del campo esterno irrotazionale possa essere espresso nella forma:

$$\boxed{ U(x) \ =\ c\ x^m }$$

con $c>0$ . Si riprendano le Eq. (6.2):

$$\begin{array}{rcl} \displaystyle \ensuremath{\frac{\partial ... ...mu \ \ensuremath{\frac{\partial^2 u}{\partial y^2}} \end{array}$$

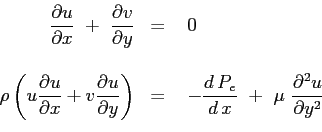
e la relazione di Bernouilli nel campo esterno allo strato limite:

$$\ensuremath{\frac{d\,P}{d\,x}}\ = \ -\ \frac{1}{2}\ \rho \ \ensuremath{\frac{d\,U^2}{d\,x}}$$

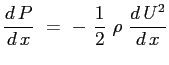
Con il profilo della velocità esterna ipotizzato si ottiene l'espressione del gradiente di pressione in funzione della velocità esterna:

$$\ensuremath{\frac{d\,P}{d\,x}} \ =\ -\ \rho \ c^2 \ m \ x^{2m +1}$$

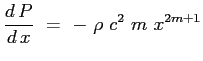
sostituendo:

$$\left( u \ensuremath{\frac{\partial u}{\partial x}} + v \ensurema... ...= c^2 \ m \ x^{2m-1}\ + \ \nu \ \ensuremath{\frac{\partial^2 u}{\partial y^2}}$$

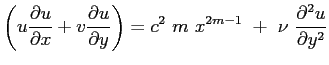
Si procede anche ora caso come nel caso della soluzione di Blasius ricorrendo all'introduzione della funzione di corrente $\Psi$ e alla adimensionalizzazione:

$$\begin{array}{rcl} u \ &=&\ \displaystyle \ensuremath{\frac{... ...le -\ \ensuremath{\frac{\partial \Psi}{\partial x}} \end{array}$$

$$\eta \ = \ \frac{y}{\delta}$$

$$= \frac{y}{\displaystyle \sqrt{\frac{\nu x}{U}}}$$

$$= \displaystyle \frac{y \sqrt{c}}{\displaystyle \sqrt{\nu}}x^{\frac{m-1}{2}}$$

$$f \ = \ \frac{\Psi}{\delta U}$$

$$= \ \frac{\Psi}{\displaystyle U \sqrt{\frac{\nu x}{U}}}$$

$$= \ \frac{\Psi}{\displaystyle \sqrt{\nu c x^{m+1}}}$$

$$\Psi \ = \ \sqrt{\nu c} \ f\ x^{\frac{m+1}{2}}$$

Si ricavano ora tutte le espressioni delle derivate da sostituire nella equazione di Prandtl con velocità esterna di Falkner-Skan:

$$\ensuremath{\frac{d\,\eta}{d\,x}} \ = \ \frac{y \sqrt{c}}{\sqrt{\nu}} \ \frac{m-1}{2} \ x^{\frac{m-3}{2}}$$

$$\ensuremath{\frac{d\,\eta}{d\,y}} \ = \ \frac{\sqrt{c}}{\sqrt{\nu}} \ x^{\frac{m-1}{2}}$$

$$\ensuremath{\frac{\partial \Psi}{\partial y}} \ = \ \ensuremath{\frac{\partial }{\partial y}}\left( \sqrt{\nu c} \ f \ x^{\frac{m+1}{2}} \right)$$

$$= \ \sqrt{\nu c} \ x^{\frac{m+1}{2}} \ \ensuremath{\frac{d\,f}{d\,\eta}} \ \ensuremath{\frac{\partial \eta}{\partial y}}$$

$$= \ \sqrt{\nu c} \ x^{\frac{m+1}{2}} \ \ensuremath{\frac{d\,f}{d\,\eta}} \ \frac{\sqrt{c}}{\sqrt{\nu}} \ x^{\frac{m-1}{2}}$$

$$= c \ \ensuremath{\frac{d\,f}{d\,\eta}} \ x^m \ = \ u$$

$$\ensuremath{\frac{\partial \Psi}{\partial x}} \ = \ \ensuremath{\frac{\partial }{\partial x}} \left( \sqrt{\nu c} \ f \ x^{\frac{m+1}{2}} \right)$$

$$= \ \sqrt{\nu c} \ \left( x^{\frac{m+1}{2}} \ \ensuremath{\frac{d\,... ...artial \eta}{\partial x}} \ + \ f \ \frac{m+1}{2} \ x^{\frac{m+1}{2}-1} \right)$$

$$= \ \sqrt{\nu c} \ \left( \ensuremath{\frac{d\,f}{d\,\eta}} \ \frac... ...-3}{2}} \ x^{\frac{m+1}{2}} \ + \ f \ \frac{m+1}{2} \ x^{\frac{m-1}{2}} \right)$$

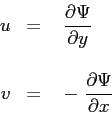
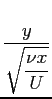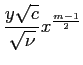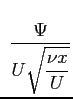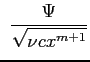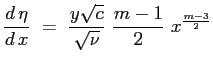
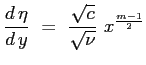
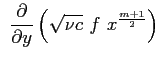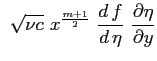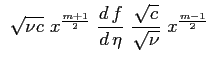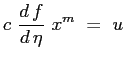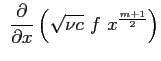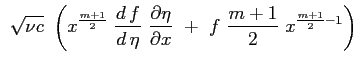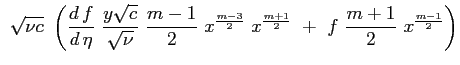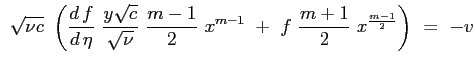$$= \ \sqrt{\nu c} \ \left( \ensuremath{\frac{d\,f}{d\,\eta}} \ \frac... ...c{m-1}{2} \ x^{m-1} \ + \ f \ \frac{m+1}{2} \ x^{\frac{m-1}{2}} \right) \ =\ -v$$ o anche elaborando ulteriormente:

$$= \ \frac{1}{2}\ \sqrt{\frac{\nu U}{x}} \ \left( \eta \ \ensuremath{\frac{d\,f}{d\,\eta}} \ (m-1) \ + \ f \right) \ =\ -v$$

$$\ensuremath{\frac{\partial^2 \Psi}{\partial x \partial y }} \ = \ \ensuremath{\frac{\partial }{\partial x}}\left(\ensuremath{\frac{\partial \Psi}{\partial y}}\right)$$

$$= \ \ensuremath{\frac{\partial }{\partial x}}\left(c \ \ensuremath{\frac{d\,f}{d\,\eta}} \ x^m\right)$$

$$= \ c \ x^m \ \ensuremath{\frac{d^2\, f}{d\, \eta^2}} \ \ensuremath{\frac{d\,\eta}{d\,x}} \ +\ c \ \ensuremath{\frac{d\,f}{d\,\eta}} \ m \ x^{m-1}$$

$$= \ c \ \left( \ensuremath{\frac{d\,f}{d\,\eta}} \ m \ x^{m-1} \ + ... ...2}} \ \frac{y \sqrt{c}}{\sqrt{\nu}} \ \frac{m-1}{2} \ x^{\frac{m-3}{2}} \right)$$

$$= \ c \ \left( \ensuremath{\frac{d\,f}{d\,\eta}} \ m \ x^{m-1} \ + ... ...}} \ \frac{y \sqrt{c}}{\sqrt{\nu}} \ \frac{m-1}{2} \ x^{\frac{3m-3}{2}} \right)$$

$$\ensuremath{\frac{\partial^2 \Psi}{\partial y^2}} \ = \ \ensuremath{\frac{\partial }{\partial y}}\left(\ensuremath{\frac{\partial \Psi}{\partial y}}\right)$$

$$= \ \ensuremath{\frac{\partial }{\partial y}}\left( c \ \ensuremath{\frac{d\,f}{d\,\eta}} \ x^m \right)$$

$$= \ c \ x^m \ \ensuremath{\frac{d^2\, f}{d\, \eta^2}} \ \frac{\sqrt{c}}{\sqrt{\nu}} \ x^{\frac{m-1}{2}}$$

$$= \ \frac{c^{\frac{3}{2}}}{\sqrt{\nu}} \ \ensuremath{\frac{d^2\, f}{d\, \eta^2}} \ x^{\frac{3m-1}{2}}$$

$$\frac{\partial^3\Psi}{\partial y^3} \ = \ \ensuremath{\frac{\partial }{\partial y}}\left( \ensuremath{\frac{\partial^2 \Psi}{\partial y^2}} \right)$$

$$= \ \frac{c^{\frac{3}{2}}}{\sqrt{\nu}} \ \frac{d^3f}{d \eta^3} \ x^{\frac{3m-1}{2}} \ \frac{\sqrt{c}}{\sqrt{\nu}} \ x^{\frac{m-1}{2}}$$

$$= \ \frac{c^2}{\nu} \ \frac{d^3f}{d \eta^3} \ x^{2m-1}$$

Si procede con la sostituzione:

$$\left( u \ensuremath{\frac{\partial u}{\partial x}} + v \ensurema... ...= c^2 \ m \ x^{2m-1}\ + \ \nu \ \ensuremath{\frac{\partial^2 u}{\partial y^2}}$$

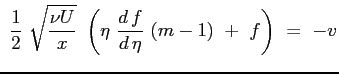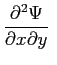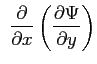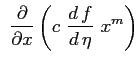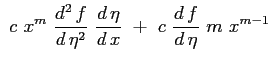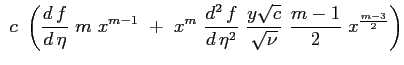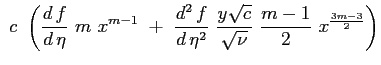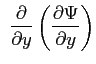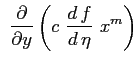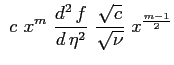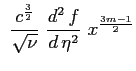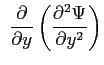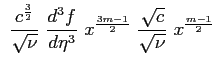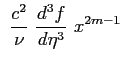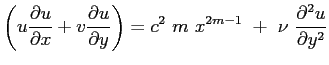
dapprima introducendo la funzione di corrente:

$$\ensuremath{\frac{\partial \Psi}{\partial y}} \ \ensuremath{\frac... ...al y^2}} \ = \ c^2 \ m \ x^{2m-1}\ + \nu \ \frac{\partial^3\Psi}{\partial y^3}$$

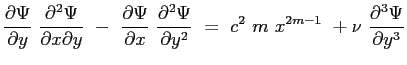
e successivamente le espressioni delle derivate:

$$\begin{split}c \ \ensuremath{\frac{d\,f}{d\,\eta}} \ x^m \ c ... ...rac{c^2}{\nu} \ \frac{d^3f}{d \eta^3} \ x^{2m-1} \\ \end{split}$$

$$\begin{split}c^2 \ x^m \ f'^2 \ m \ x^{m-1} \ + \ c^2 \ x^m \... ...\ c^2 \ m \ x^{2m-1} \ + \ c^2 \ x^{2m-1} \ f^{'''} \end{split}$$

$$\begin{split}f'^2 \ m \ x^{2m-1} \ + \ f' \ f'' \ \frac{m-1}{... ...}} \ = \\ = \ m \ x^{2m-1} \ + \ x^{2m-1} \ f^{'''} \end{split}$$

moltiplicando tutto per $x^{-(2m-1)}$

$$\begin{split}f'^2 \ m \ + \ f' \ f'' \ \frac{m-1}{2} \ \eta \... ...\ x^{2m-1} \ x^{-(2m-1)} \ = \\ = \ m \ + \ f^{'''} \end{split}$$

$$f'^2 \ m \ - \ f \ f'' \ \frac{m+1}{2} \ = \ m \ + \ f^{'''}$$

e finalmente:

$$\boxed{ f^{'''} \ + \ f \ f'' \ \frac{m+1}{2} \ - \ f'^2 \ m \ + \ m \ = \ 0 }$$ (8.1)

   c.c.$$\left\{ \begin{array}{rcll} f(\eta=0) &=& 0 & \mbox{portata a... ...w& 1 & \mbox{$u=U$ nel campo irrotazionale} \end{array}\right.$$

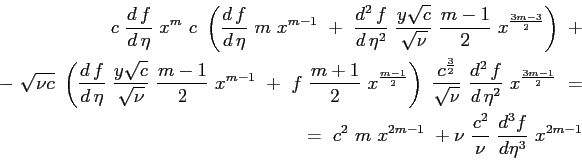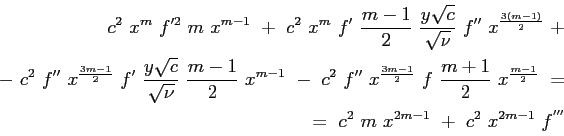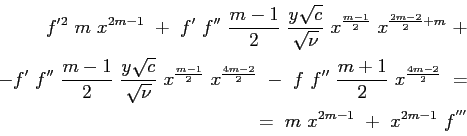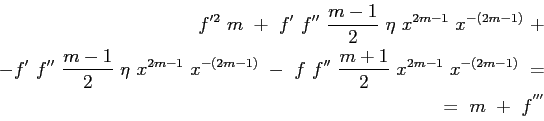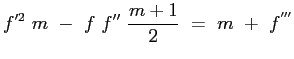che con il valore $m=0$ esprime nuovamente la Eq. (7.2) di Blasius.