



Next: Soluzione
Up: Il metodo di Runge-Kutta
Previous: Metodo di Runge-Kutta del
Indice
Dai ragionamenti fatti si può intuire che l'ordine del metodo può essere aumentato al fine di aumentarne l'accuratezza. Il metodo più usato è quello del quarto ordine7.6:
![\begin{displaymath}\begin{array}{rcl} k_1 & = & f(x_n,y_n) \\ [3pt]\\ k_2 & = & ...
...+ \frac{k_3}{3} + \frac{k_4}{6} + \circ(h^5)\right) \end{array}\end{displaymath}](img788.png) |
(7.4) |
in cui:
![$ [k_1]$](img789.png) è la pendenza della curva all'inizio dell'intervallo;
è la pendenza della curva all'inizio dell'intervallo;
![$ [k_2]$](img790.png) è la pendenza nel punto medio dell'intervallo con
è la pendenza nel punto medio dell'intervallo con 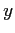 calcolato usando il valore
calcolato usando il valore 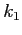 ;
;
![$ [k_3]$](img792.png) è la pendenza nel punto medio dell'intervallo con
è la pendenza nel punto medio dell'intervallo con 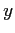 calcolato usando il valore
calcolato usando il valore 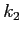 ;
;
![$ [k_4]$](img794.png) è la pendenza della curva all'estremità dell'intervallo col valore di
è la pendenza della curva all'estremità dell'intervallo col valore di 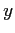 calcolato usando
calcolato usando 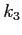 .
.
Si riporta di seguito la lista di comandi per il software ``Octave'' per la costruzione di una funzione RK-4:
![\begin{VerbatimProg}
\par
function [tout, yout] = rk4(FunFcn, tspan, y0, ssize)
...
...+ 2*s3 +s4)/6;
t = tout(k);
yout(k,:) = y.';
\par
end;
\par
\end{VerbatimProg}](img796.png)
2009-01-26
![\begin{displaymath}\begin{array}{rcl} k_1 & = & f(x_n,y_n) \\ [3pt]\\ k_2 & = & ...
...+ \frac{k_3}{3} + \frac{k_4}{6} + \circ(h^5)\right) \end{array}\end{displaymath}](img788.png)
![\begin{displaymath}\begin{array}{rcl} k_1 & = & f(x_n,y_n) \\ [3pt]\\ k_2 & = & ...
...+ \frac{k_3}{3} + \frac{k_4}{6} + \circ(h^5)\right) \end{array}\end{displaymath}](img788.png)
![\begin{VerbatimProg}
\par
function [tout, yout] = rk4(FunFcn, tspan, y0, ssize)
...
...+ 2*s3 +s4)/6;
t = tout(k);
yout(k,:) = y.';
\par
end;
\par
\end{VerbatimProg}](img796.png)