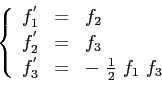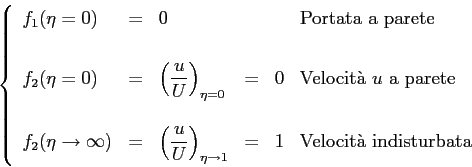Soluzione

Si è detto che il metodo RK-4 permette di risolvere poroblemi ai valori iniziali. Visto che la terza condizione del sistema di primo ordine non è una condizione iniziale, il metodo numerico sarà applicato per tentativi fino alla sua convergenza. Si immetteranno cioè valori di tentativo della 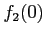$f_2(0)$ fino a verificare il valore di $f_2(\eta=\infty)=1$ .

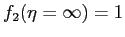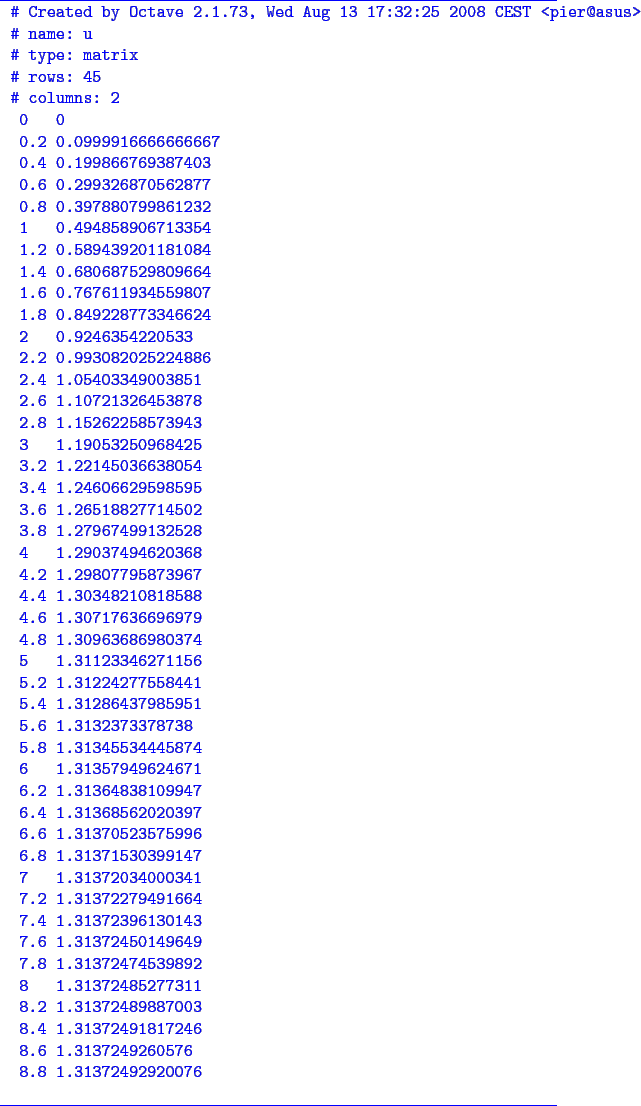
Si riporta sotto il listato dei comandi per il programma ``Octave'' per la risoluzione del sistema:

$$f \ =\ f_1$$

$$\left\{ \begin{array}{rcl} f_1^{'} & = & f_2 \\ f_2^{'} & =... ... f_3^{'} & = & - \ \frac{1}{2} \ f_1 \ f_3 \end{array}\right.$$

con le condizioni al contorno:

   c.c.$$\left\{ \begin{array}{lclcll} \displaystyle f_1(\eta=0) & = ... ...ow 1}&=& 1 & \mbox{Velocit\\lq a indisturbata} \end{array}\right.$$

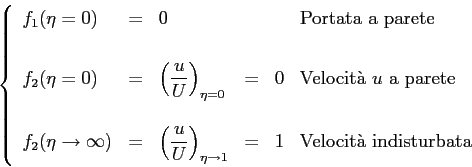
Figura 7.5: Andamento di 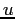$u$ con $f_2(0)=0.5$ .

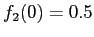Figura 7.6: Andamento di 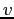$v$ con $f_2(0)=0.5$ .

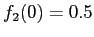I risultati numerici con il valore di tentativo 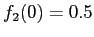$f_2(0)=0.5$ della velocità $u$ :

e della velocità 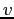$v$ tenendo conto della Eq. (7.1):

Ripetendo i calcoli e affinando il valore della 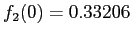$f_2(0)=0.33206$ si perviene al risultato definitivo per

Figura 7.7: Andamento di 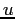$u$ per $f_2(0)=0.33206$ .

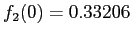Figura 7.8: Andamento di 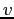$v$ per $f_2(0)=0.33206$ .

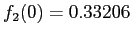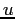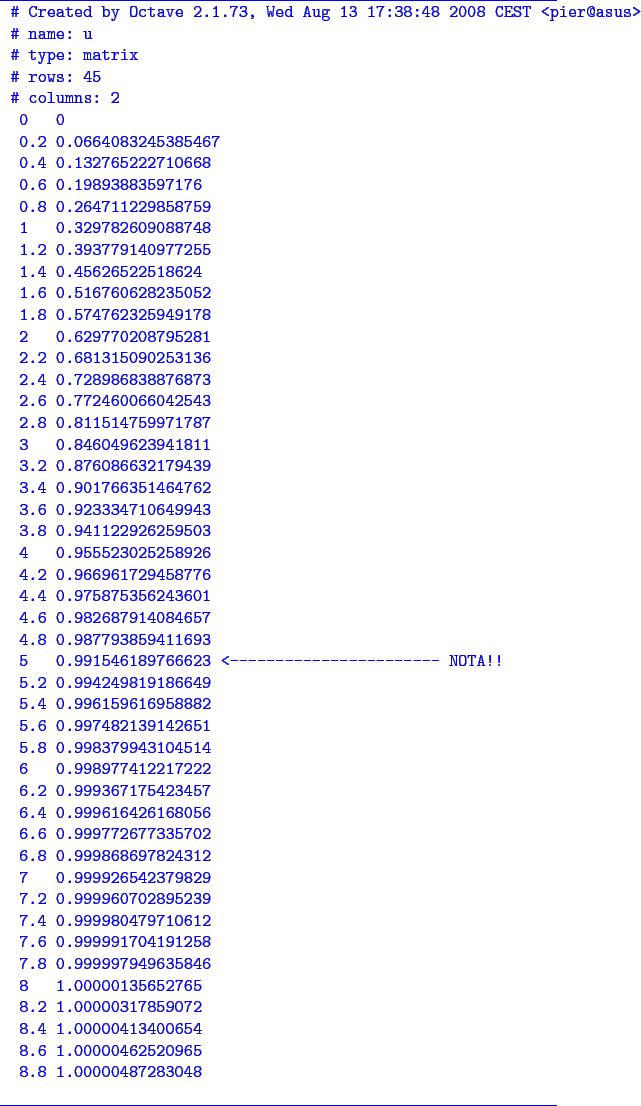
la velocità $u$ :

Si nota come per il valore 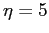$\eta=5$ la velocità raggiunge il 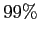$99\%$ della velocità indisturbata. Si ottiene quindi la velocità 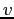$v$ ottenuta ricorrendo alla Eq. (7.1):

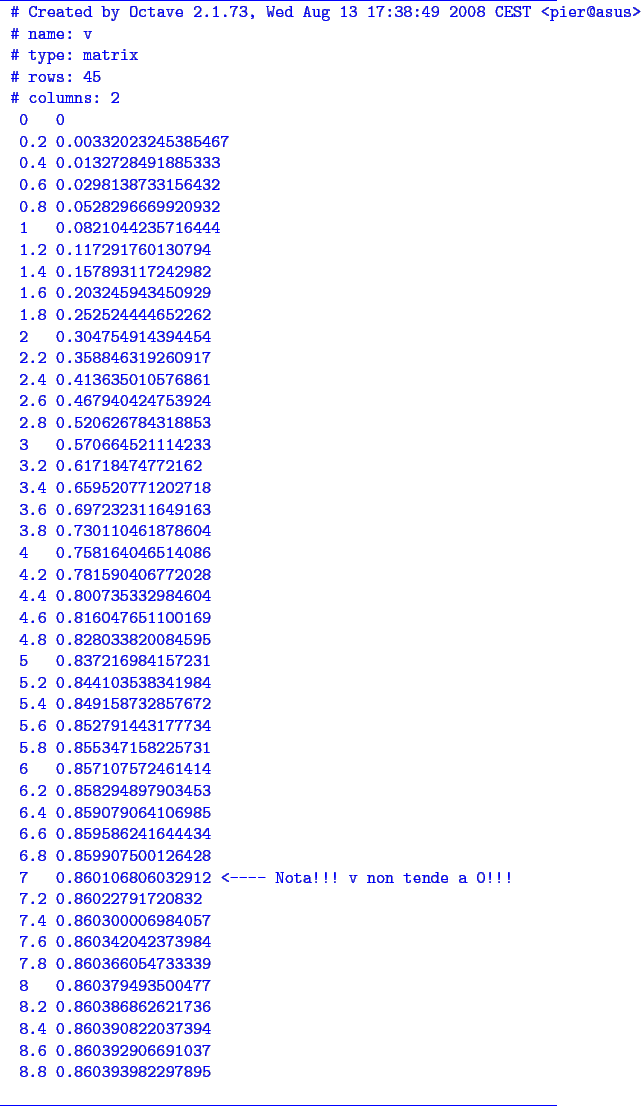
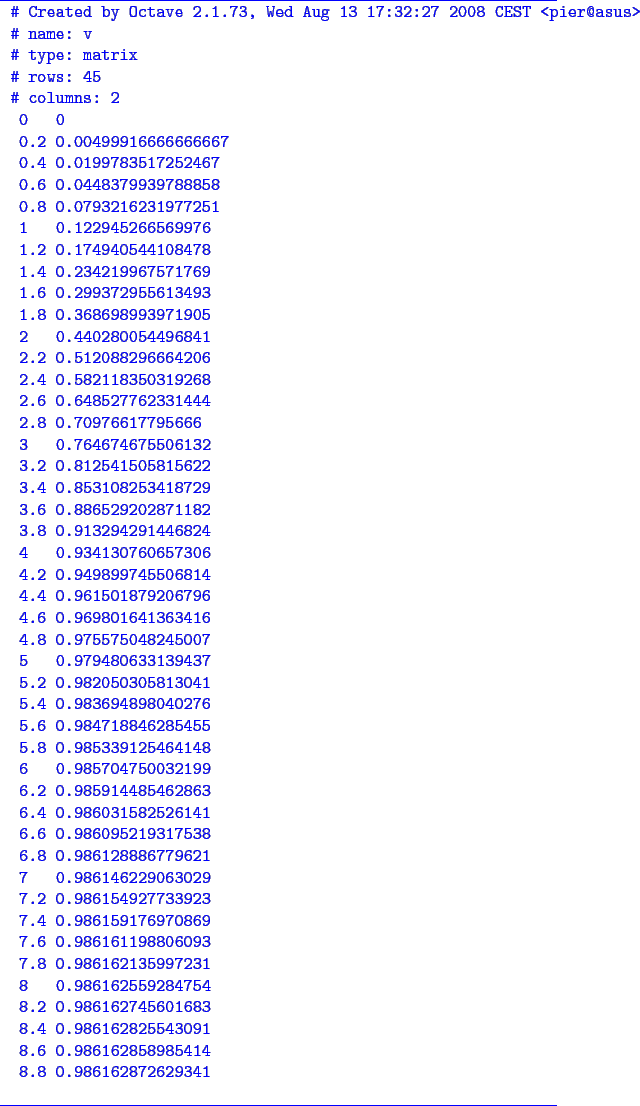
La tabella dei risultati numerici complessivi: