Metodo di Runge-Kutta del secondo ordine

Next: Metodo di Runge-Kutta del Up: Il metodo di Runge-Kutta Previous: Instabilità numerica Indice

Metodo di Runge-Kutta del secondo ordine

**Figura 7.4:** Runge Kutta del II ordine.
$\includegraphics[width=75mm]{RK2.eps}$

Si è visto come nel metodo di Eulero venga introdotto un elevato errore di troncamento a causa della valutazione della pendenza della curva all'inizio 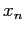di ciascun passo di integrazione. A causa di questo il metodo di Eulero è molto asimmetrico nel suo procedere dall'inizio alla fine dell'intervallo di integrazione. Si può cercare di migliorare il metodo adottando un approccio più simmetrico valutando con il metodo di Eulero la pendenza nel punto medio del passo di integrazione ed utilizzando questa informazione per ottenere il valore della funzione all'estremità del passo:

$\displaystyle k_1 = f(x_n,y_n)$

$\displaystyle k_2 = f(x_n + h/2,y_n+ h\, k_1/2)$

$\displaystyle y_{n+1} = y_n + h\, k_2 + \circ(h^3)$

Così facendo si annulla l'errore del primo ordine ottenendo così un metodo del secondo ordine. Il metodo di Eulero può essere considerato un metodo di Runge Kutta del primo ordine.

2009-01-26