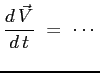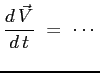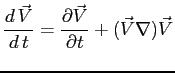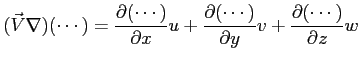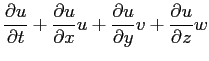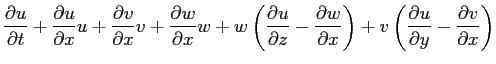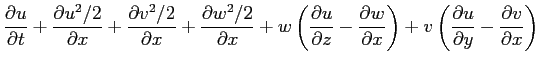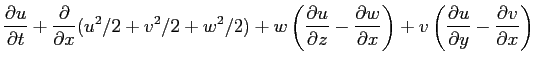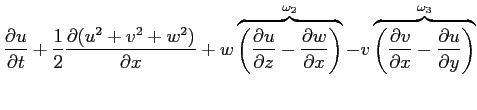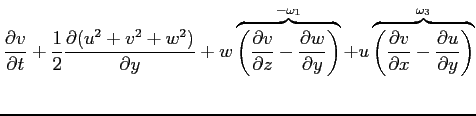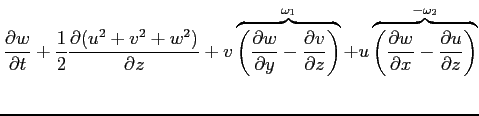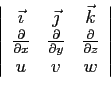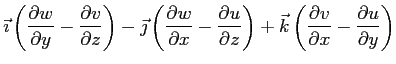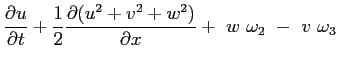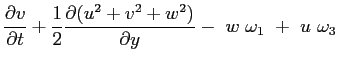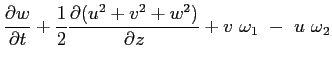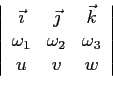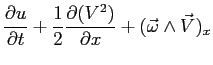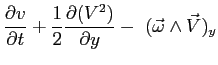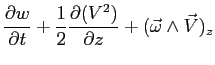Next: Cinematica dei fluidi: relazioni
Up: Forma differenziale lagrangiana delle
Previous: Forma differenziale lagrangiana delle
Indice
Ci si propone di trovare una espressione della derivata totale lagrangiana di una funzione vettoriale.
Per semplicità si può procedere con una componente:
In forma vettoriale, considerando analoghe relazioni per le rimanenti componenti:
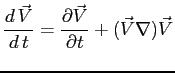 |
(2.14) |
in cui l'operatore:
o anche:
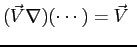
grad
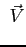
Una ulterire manipolazione permette di mettere in risalto le componenti di rotazione del moto.
Al secondo membro delle equazioni di sopra si riconosce la presenza di termini del rotore del vettore 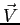 :
:
A questo punto sono evidenti al secondo membro delle equazioni sopra i termini del prodotto vettoriale
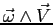 :
:
Si può riscrivere:
e in definitiva:
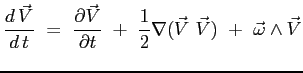 |
(2.15) |
La Eq. (2.15) permette allora la scrittura della Eq. (2.13).




Next: Cinematica dei fluidi: relazioni
Up: Forma differenziale lagrangiana delle
Previous: Forma differenziale lagrangiana delle
Indice
2009-01-26