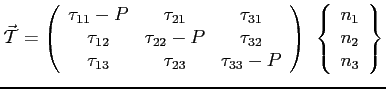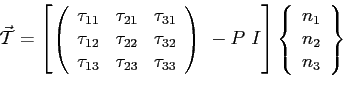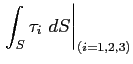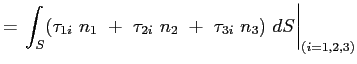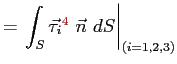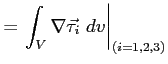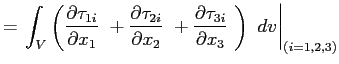Risultante delle forze tangenziali

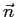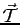Si consideri un elemento di superficie unitaria individuato come in Fig. 2.1 di normale $\vec{n}$ . Sia $\vec{\mathcal T}$ il vettore risultante degli sforzi di superficie agenti sulla faccia di normale 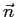$\vec{n}$ . Si indichi inoltre con:

$$\tau_{ij}$$

la componente dello sforzo di superficie agente sulla faccia di normale 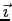$\vec{\imath}$ che spira nella direzione $j$ .

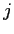Figura 2.1: Tetraedro elementare.

L'equilibrio^2.3 del tetraedro porta alla:

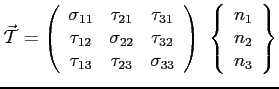$$\vec{\mathcal T}=\left( \begin{array}{ccc} \sigma_{11} & \tau_{21... ...d{array} \right)\ \left\{ \begin{array}{c} n_1\\ n_2\\ n_3 \end{array} \right\}$$ (2.4)

Il tensore degli sforzi superficiali che compare nella Eq. (2.4) è simmetrico in virtù del teorema di reciprocità di Cauchy Eq. (B.6).
È da osservare che le componenti di sforzo normale 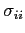$\sigma_{ii}$ contengono due contributi:

1. Un contributo idrostatico dovuto alla pressione del fluido circostante 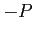$-P$ , del quale si è già tenuto conto in precedenza nell'Eq. (2.3), negativo in quanto opposto al versore $\vec{n}$ ;
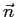2. Un contributo di sforzo viscoso 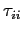$\tau_{ii}$ dovuto all'espansione o contrazione del volume elementare;

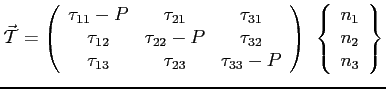$$\vec{\mathcal T}=\left( \begin{array}{ccc} \tau_{11}-P & \tau_{21... ...d{array} \right)\ \left\{ \begin{array}{c} n_1\\ n_2\\ n_3 \end{array} \right\}$$ (2.5)

$$\vec{\mathcal T}=\left[ \left( \begin{array}{ccc} \tau_{11} ... ...left\{ \begin{array}{c} n_1\\ n_2\\ n_3 \end{array}\right\}$$

Si può ora esplicitare l'integrale di superficie relativo alle forze tangenziali nelle tre direzioni:

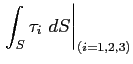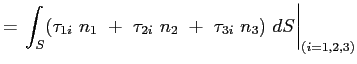$$\left.\int_S \tau_i\ dS\right\vert _{(i=1,2,3)} =\left. \int_S(\tau_{1i}\ n_1\ +\ \tau_{2i}\ n_2\ +\ \tau_{3i}\ n_3)\ dS\right\vert _{(i=1,2,3)}$$ (2.6)

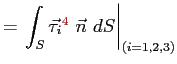$$= \left. \int_S \vec{\tau_i}\footnotemark \ \vec{n}\ dS \right\vert _{(i=1,2,3)}$$ (2.7) ^2.4

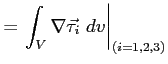$$=\left. \int_V \nabla \vec{\tau_i}\ dv\right\vert _{(i=1,2,3)}$$ (2.8)

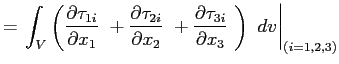$$=\left. \int_V \left( \ensuremath{\frac{\partial \tau_{1i}}{\part... ...{\frac{\partial \tau_{3i}}{\partial x_3}}\ \right)\ dv \right\vert _{(i=1,2,3)}$$ (2.9)