Forma differenziale euleriana delle equazioni di Navier-Stokes

L'espressione integrale in termini di integrali di volume:

$$\ensuremath{\frac{\partial }{\partial t}}\int_V\rho\ u_i\ dv\ + \... ...2}} + \ensuremath{\frac{\partial (\rho \ u_i \ u_3)}{\partial x_3}} \right)\ dv =$$

$$\left. \int_V \gamma_i\ dv - \int_V \ensuremath{\frac{\partial P}{\partial x_i}}\ dv + \int_V\nabla \vec{\tau_i}\ dv \right\vert _{(i=1,2,3)}$$

Adottando la notazione tensoriale di variazione degli indici:

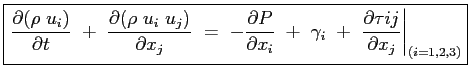$$\fbox{$ \displaystyle \left. \ensuremath{\frac{\partial (\rho\ u_... ...\ensuremath{\frac{\partial \tau{ij}}{\partial x_j}} \right\vert _{(i=1,2,3)} $}$$ (2.10)

Si può ottenere la forma compatta vettoriale:

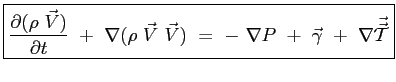$$\fbox{$ \displaystyle \ensuremath{\frac{\partial (\rho\ \vec{V})}... ...c{V})}\ = \ -\ \nabla P\ +\ \vec{\gamma} \ + \ \nabla \vec{\vec{\mathcal T}} $}$$ (2.11)

in cui si è posto:

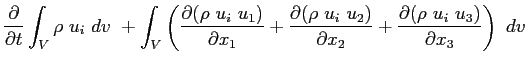
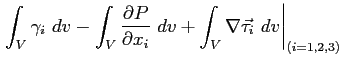
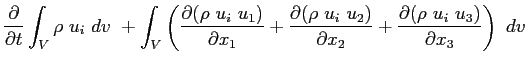
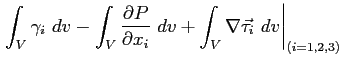
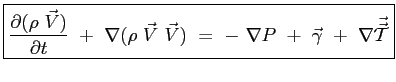
$$\nabla{(\rho\ \vec{V}\ \vec{V})}\ = \ \left[ \ensuremath{\frac{\partial (\rho u_1 u_1)}{\partial x_1}... ...uremath{\frac{\partial (\rho u_3 u_1)}{\partial x_3}}\right]\ \vec{\imath_1}\ +$$

$$\ \left[ \ensuremath{\frac{\partial (\rho u_1 u_2)}{\partial x_1}... ...uremath{\frac{\partial (\rho u_3 u_2)}{\partial x_3}}\right]\ \vec{\imath_2}\ +$$

$$\ \left[ \ensuremath{\frac{\partial (\rho u_1 u_3)}{\partial x_1}... ...ensuremath{\frac{\partial (\rho u_3 u_3)}{\partial x_3}}\right]\ \vec{\imath_3}$$

e:

$$\nabla \vec{\vec{\mathcal T}} \ = \ \left[ \ensuremath{\frac{\partial \tau_{11}}{\partial x_1}}+\en... ...+\ensuremath{\frac{\partial \tau_{31}}{\partial x_3}}\right]\ \vec{\imath_1}\ +$$

$$\ \left[ \ensuremath{\frac{\partial \tau_{12}}{\partial x_1}}+\en... ...+\ensuremath{\frac{\partial \tau_{32}}{\partial x_3}}\right]\ \vec{\imath_2}\ +$$

$$\ \left[ \ensuremath{\frac{\partial \tau_{13}}{\partial x_1}}+\en... ...2}}+\ensuremath{\frac{\partial \tau_{33}}{\partial x_3}}\right]\ \vec{\imath_3}$$