



Next: Errori numerici
Up: Il metodo di Runge-Kutta
Previous: Il metodo di Runge-Kutta
Indice
Nel metodo di Eulero7.4 la soluzione avanza, una volta nota al passo 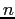 nella stazione
nella stazione
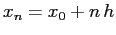 , al passo
, al passo 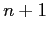 nella stazione
nella stazione
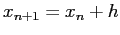 :
:
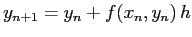 |
(7.3) |
Figura 7.3:
Passi nel metodo di Eulero
|
|
La Eq. (7.3) è una tipica formula ``non simmetrica'', nel senso che sfrutta informazioni, le derivate
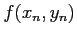 , valutate solo al primo estremo dell'intervallo
, valutate solo al primo estremo dell'intervallo
![$ [x_n , x_{n+1}]$](img754.png) . Ciò rende la ``predizione'' del valore
. Ciò rende la ``predizione'' del valore 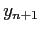 accurata a meno di un termine di correzione di
accurata a meno di un termine di correzione di
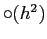 . La formula di Eulero corrisponde quindi ad un metodo del primo ordine7.5.
Il metodo di Eulero non è raccomandabile per un uso pratico per due motivi principali:
. La formula di Eulero corrisponde quindi ad un metodo del primo ordine7.5.
Il metodo di Eulero non è raccomandabile per un uso pratico per due motivi principali:
- non è accurato, a parità di passo di integrazione, quanto altri metodi di altrettanto semplice implementazione, come il metodo di Runge-Kutta;
- il metodo di Eulero può risultare spesso instabile quando la funzione
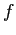 è sensibilmente variabile.
è sensibilmente variabile.




Next: Errori numerici
Up: Il metodo di Runge-Kutta
Previous: Il metodo di Runge-Kutta
Indice
2009-01-26