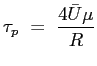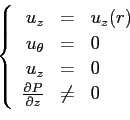
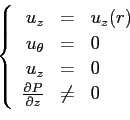
![\begin{displaymath}
\begin{array}{rcl}
0&=&\displaystyle -\ensuremath{\frac{\par...
...ath{\frac{\partial u_z}{\partial z}}&=&0\\ [3pt]\\
\end{array}\end{displaymath}](img334.png)
dalle quali si vede che la pressione è funzione della sola coordinata z:
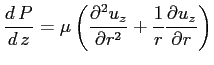
L'equazione sopra ha senso solo se:
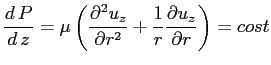
Si vede quindi che la pressione ha un andamento lineare, decrescente se il fluido si muove nel verso positivo delle
Se si ragiona in termini di pressione relativa si può porre
con:
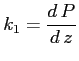
Si può ricavare l'andamento della velocità :
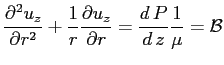
con le condizioni al contorno di aderenza a parete e di simmetria cilindrica del profilo di velocità :
![\begin{displaymath}
\left\{
\begin{array}{lll}
u_z(R)&=&0 \\ [3pt]\\
\displayst...
...math{\frac{d\,u_z}{d\,r}}\right)_{r=0}&=&0
\end{array}\right.
\end{displaymath}](img343.png)
L'equazione sopra può essere ricondotta ad una ``equazione lineare''4.1 del primo ordine:
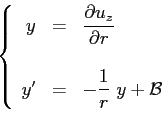
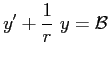
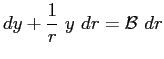
L'equazione lineare va risolta cercando una funzione ausiliaria
![$\displaystyle d[I(r)y]= I(x) dy + I(x)\ \frac{1}{r}\ y \ dr $](img350.png)
quindi:
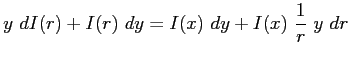
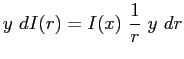
e imponendo la condizione
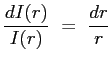
che integrata da:
Moltiplicando l'equazione di partenza per
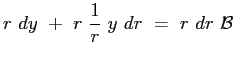
che viene facilmente integrata:
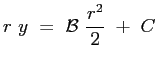
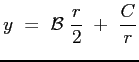
La costante di integrazione viene calcolata imponendo l'annullamento della derivata della velocità , ossia
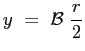
Procedendo alla successiva integrazione:
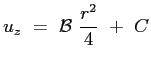
La costante
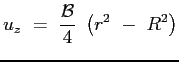
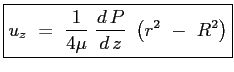 |
(4.5) |
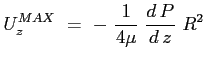
La velocità media nel condotto:
![$\displaystyle \pi\ R^2 \ \bar{U}\ =\ \frac{1}{4\mu}\ \ensuremath{\frac{d\,P}{d\,z}}\
\int_0^R{[(r^2-R^2)\ 2\ \pi\ r\ ] dr}
$](img370.png)
che elaborata porta a:
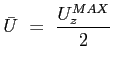
Il valore dello sforzo tangenziale a parete:
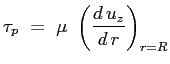
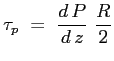
Sostituendo in questa l'espressione del gradiente di pressione ricavato dall'espressione della velocità massima presa in valore assoluto: