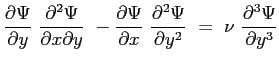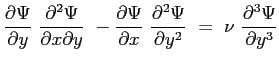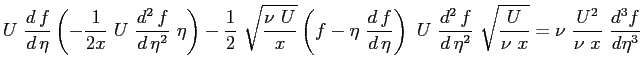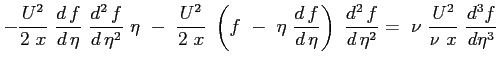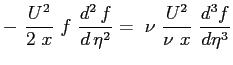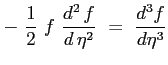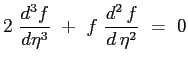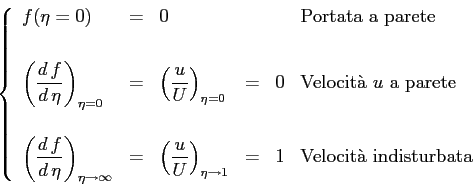Next: Risoluzione dell'equazione di Blasius
Up: Equazione di Blasius: soluzione
Previous: La funzione di corrente
Indice
Sostituendo le espressioni trovate nella equazione principale:
Si ottiene finalmente l'equazione di Blasius:
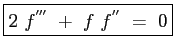 |
(7.2) |
con le condizioni al contorno:
c.c.
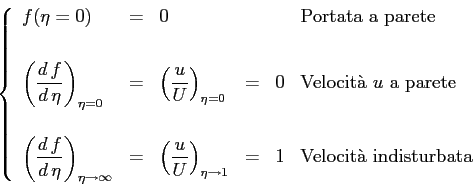
2009-01-26