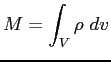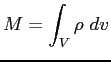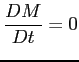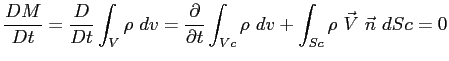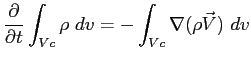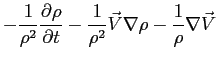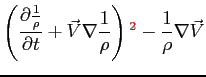Forme lagrangiana ed euleriana

L'equazione di continuità esprime la conservazione della massa all'interno di un volume di controllo che non scambia materia con l'esterno. La massa contenuta all'interno di un dato volume 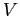$V$ risulta data dalla:

$$M=\int_{V}\rho \ dv$$

Inseguendo il volume in questione, la equazione di continuità in forma integrale Lagrangiana risulta espressa dalla:

$$\frac{DM}{Dt}=0$$

Applicando la Eq. (B.1) si ha:

$$\frac{DM}{Dt}=\frac{D}{Dt}\int_{V}\rho \ dv= \frac{\partial}{\partial t}\int_{Vc}\rho \ dv + \int_{Sc}\rho \ \vec{V}\ \vec{n}\ dSc=0$$

ne deriva la equazione di continuità Euleriana in forma integrale:

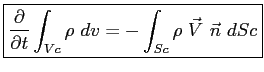$$\fbox{$ \displaystyle \frac{\partial}{\partial t}\int_{Vc}\rho \ dv=-\int_{Sc}\rho \ \vec{V} \ \vec{n}\ dSc $}$$ (1.1)

La forma differenziale dell'equazione di continuità Euleriana si ottiene applicando alla Eq. (1.1) il teorema del flusso di Gauss^1.1:

$$\frac{\partial}{\partial t}\int_{Vc}\rho \ dv=-\int_{Vc}\nabla (\rho\vec{V}) \ dv$$

Dall'equazione sopra discende la:

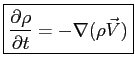$$\fbox{$\displaystyle \frac{\partial\rho}{\partial t}=-\nabla (\rho\vec{V})$}$$ (1.2)

Manipolando la Eq. (1.2) si ottiene la sua forma Lagrangiana differenziale.

$$\frac{\partial\rho}{\partial t} = -\nabla (\rho\vec{V})$$

$$= -\rho \ \nabla(\vec{V}) - \vec{V} \ \nabla(\rho)$$

$$\frac{\partial\rho}{\partial t}+\rho \ \nabla(\vec{V}) + \vec{V} \ \nabla(\rho) =0$$ (1.3)

dividendo la Eq. (1.3) pe 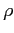$\rho$ si ottiene la:

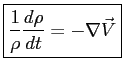$$\fbox{$ \displaystyle \frac{1}{\rho}\frac{d\rho}{dt}=-\nabla\vec{V}$}$$ (1.4)

dividendo invece la Eq. (1.3) per 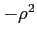$-\rho^2$ si ottiene:

$$-\frac{1}{\rho^2}\frac{\partial\rho}{\partial t}-\frac{1}{\rho^2}\vec{V}\nabla\rho-\frac{1}{\rho}\nabla\vec{V} =$$ 0

$$\left(\frac{\partial\frac{1}{\rho}}{\partial t}+\vec{V}\nabla\frac{1}{\rho}\right)\footnotemark -\frac{1}{\rho}\nabla\vec{V} =$$ 0   ^1.2

$$\frac{d\frac{1}{\rho}}{dt} = \frac{1}{\rho}\nabla\vec{V}$$ (1.5)

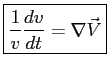$$\fbox{$ \displaystyle \frac{1}{v}\frac{dv}{dt} = \nabla\vec{V}$}$$ (1.6)

Le Eq. (1.4) e Eq. (1.6) rappresentano entrambe la equazione di continuità in forma differenziale Lagrangiana ed evidenziano rispettivamente che la divergenza con segno del vettore velocità 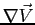$\nabla\vec{V}$ rappresenta il tasso di compressione o dilatazione nel tempo della particella fluida.