



Next: Teorema di Gauss
Up: Teoremi utili
Previous: Teoremi utili
Indice
Il teorema di trasformazione di Reynolds è di fondamentale importanza. Esso permette di passare facilmente dall'espressione generica del teorema della quantità di moto alla sua versione sotto la forma delle equazioni di Navier-Stokes.
La derivata totale, ossia Lagrangiana di una grandezza viene in virtù di tale teorema, espressa in termini delle sue componenti parziali.
Teorema -thm
(di Reynolds)
Sia 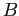 una grandezza estensiva legata a
una grandezza estensiva legata a 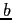 intensiva che ne rappresenta il valore per unità di volume di controllo
intensiva che ne rappresenta il valore per unità di volume di controllo 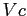 avente superficie di contorno
avente superficie di contorno 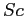 :
:
e
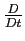 la derivata totale o Lagrangiana di
la derivata totale o Lagrangiana di 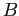 :
:
allora:
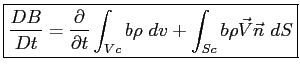 |
(B.1) |
La derivata totale di una grandezza intensiva computata su di un volume di controllo 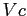 viene vista come somma della variazione della grandezza nel suo volume di controllo nel tempo, e del flusso netto della grandezza stessa attaverso ila superficie di controllo che racchiude il volume. In questo modo il punto di osservazione si sgancia dal volume di controllo in moto
viene vista come somma della variazione della grandezza nel suo volume di controllo nel tempo, e del flusso netto della grandezza stessa attaverso ila superficie di controllo che racchiude il volume. In questo modo il punto di osservazione si sgancia dal volume di controllo in moto 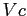 che racchiude la grandezza estensiva (punto di vista Lagrangiano) e passa ad un volume di controllo fisso nello spazio
che racchiude la grandezza estensiva (punto di vista Lagrangiano) e passa ad un volume di controllo fisso nello spazio 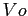 rispetto al quale vengono espresse le componenti di derivazione parziale (punto di vista Euleriano)B.1.
rispetto al quale vengono espresse le componenti di derivazione parziale (punto di vista Euleriano)B.1.
Figura B.1:
Volume di controllo 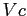 tra gli istanti iniziale e finale di osservazione.
tra gli istanti iniziale e finale di osservazione.
|
|
Si segua il volume di controllo 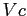 tra gli istanti
tra gli istanti 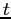 e
e 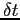 . Guardando la Fig. B.1 si vede che se si considera lo spostamento infinitesimo subito nella sua evoluzione da
. Guardando la Fig. B.1 si vede che se si considera lo spostamento infinitesimo subito nella sua evoluzione da 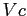 , si potrà individuare una zona di sovrapposizione
, si potrà individuare una zona di sovrapposizione 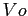 , una zona competente a
, una zona competente a 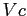 osservato all'istante
osservato all'istante 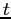 indicata con
indicata con 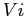 ed una zona competente a
ed una zona competente a 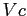 osservato all'istante
osservato all'istante
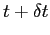 indicata con
indicata con 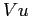 . Queste due zone,
. Queste due zone, 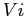 e
e 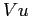 possono essere viste rispettivamente come volumi in ingresso e in uscita della grandezza intensiva nel volume
possono essere viste rispettivamente come volumi in ingresso e in uscita della grandezza intensiva nel volume 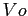 visto come fisso nell'intervallo di tempo
visto come fisso nell'intervallo di tempo 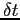 . La grandezza estensiva
. La grandezza estensiva 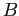 espressa nell'istante iniziale sarà :
espressa nell'istante iniziale sarà :
e nell'istante finale:
La derivata totale della grandezza 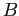 sarà dunque:
sarà dunque:
Se si introduce l'ipotesi di considerare 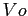 B.2 costante nel tempo allora:
B.2 costante nel tempo allora:
Per quanto riguara gli integrali di volume su 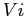 e
e 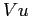 , integrando per fili su
, integrando per fili su 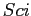 ed
ed 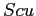 , ossia le porzioni di superficie di controllo
, ossia le porzioni di superficie di controllo 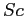 del volume fisso
del volume fisso 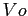 attraverso cui entra ed esce il flusso della grandezza
attraverso cui entra ed esce il flusso della grandezza 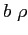 :
:
si ottiene:
avendo adottato la convenzione secondo la quale il versone normale 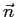 è positivo se uscente dalla superficie, ossia:
è positivo se uscente dalla superficie, ossia:
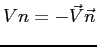
su
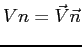
su
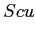
Da quanto sopra risulta quindi dimostrata l'Eq. (B.1).




Next: Teorema di Gauss
Up: Teoremi utili
Previous: Teoremi utili
Indice
2009-01-26
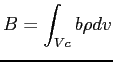
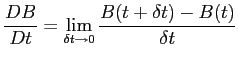
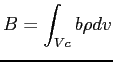
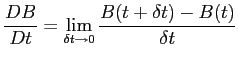
![]() tra gli istanti
tra gli istanti ![]() e
e ![]() . Guardando la Fig. B.1 si vede che se si considera lo spostamento infinitesimo subito nella sua evoluzione da
. Guardando la Fig. B.1 si vede che se si considera lo spostamento infinitesimo subito nella sua evoluzione da ![]() , si potrà individuare una zona di sovrapposizione
, si potrà individuare una zona di sovrapposizione ![]() , una zona competente a
, una zona competente a ![]() osservato all'istante
osservato all'istante ![]() indicata con
indicata con ![]() ed una zona competente a
ed una zona competente a ![]() osservato all'istante
osservato all'istante
![]() indicata con
indicata con ![]() . Queste due zone,
. Queste due zone, ![]() e
e ![]() possono essere viste rispettivamente come volumi in ingresso e in uscita della grandezza intensiva nel volume
possono essere viste rispettivamente come volumi in ingresso e in uscita della grandezza intensiva nel volume ![]() visto come fisso nell'intervallo di tempo
visto come fisso nell'intervallo di tempo ![]() . La grandezza estensiva
. La grandezza estensiva ![]() espressa nell'istante iniziale sarà :
espressa nell'istante iniziale sarà :
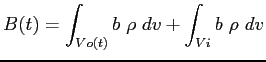
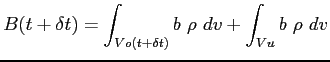
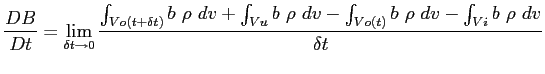
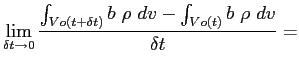
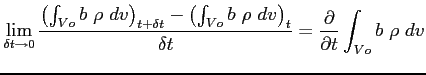
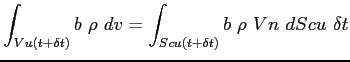
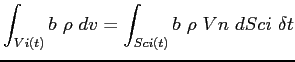
![$\displaystyle \lim_{\delta t \rightarrow 0}\left[\frac{\int_{Scu}b \ \rho \ \ve...
...{V} \ dSci}{\delta t}\right]\delta t=\int_{Sc}b \ \rho \ \vec{n} \vec{V} \ dSc
$](img1159.png)