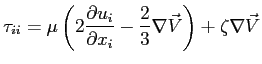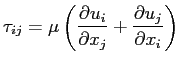Fluido compressibile

Se il fluido è compressibile le forze viscose che nascono al suo interno possono essere imputate non solo alla sua distorsione ma anche alla possibilità di un suo cambiamento di volume. Il volumetto elementare di fluido può subire due tipi di deformazione: la distorsione (variazione di forma) e la variazione di volume. A queste possono essere associate due tipi di viscosità : la viscosità dinamica 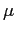$\mu$ shear viscosity e la viscosità di volume 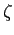$\zeta$ bulk viscosity. La viscosità di volume è di difficile misurazione e in genere piccola.
Il termine di variazione di volume è rappresentato dalla divergenza della velocità 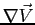$\nabla\vec{V}$ che rappresenta la traccia del tensore delle velocità di deformazione. Quest ultimo può essere spezzato in due tensori. Il primo a traccia nulla rappresenta la deformazione pura, il secondo la variazione di volume.

$${\vec{V}\ =}$$

$$\overbrace{\vec{V}_0\ + \vec{\Omega}\ \wedge \vec{V}}^{\emph{termini di spostamento rigido}} +$$

$$\frac{1}{2}\overbrace{\left(\ \begin{array}{ccc} \left( 2 \e... ...end{array}\right)}^{\emph{termini di deformazione pura}} (P-O)+$$

$$\frac{1}{3} \overbrace{\left( \begin{array}{ccc} \nabla \vec{... ... \end{array}\right)}^{\emph{termini di dilatazione pura}} (P-O)$$

L'espressione degli sforzi tangenziali diviene allora:

$$\tau_{ii}=\mu \left( 2 \ensuremath{\frac{\partial u_i}{\partial x_i}}-\frac{2}{3}\nabla \vec{V}\right) + \zeta \nabla \vec{V}$$

e:

$$\tau_{ij}=\mu \left(\ensuremath{\frac{\partial u_i}{\partial x_j}}+\ensuremath{\frac{\partial u_j}{\partial x_i}}\right)$$

L'espressione generale può essere scritta ricorrendo alla notazione 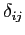$\delta_{ij}$ di Kroneker^2.10:

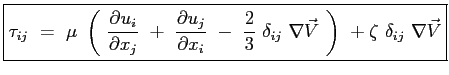$$\displaystyle \fbox{$ \tau_{ij}\ =\ \mu\ \left(\ \displaystyle \e... ...\delta_{ij}\ \nabla \vec{V}\ \right)\ + \zeta \ \delta_{ij} \ \nabla \vec{V} $}$$ (2.17)