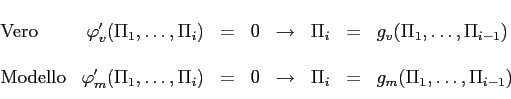Un esempio importante di analogia è quello sussistente tra modello matematico e modello fisico.
Il modello matematico di un sistema fisico è dato dal numero minimo di equazioni differenziali con le relative condizioni al contorno ed iniziali la cui soluzione fornisce un'insieme di funzioni capaci di descrivere completamente l'evoluzione spazio-temporale del sistema.
Dati quindi due sistemi fisici, ``vero'' e ``modello'' in similitudine fisica, ad essi saranno associati due modelli matematici che, adimensionalizzati, risulteranno identici. Si intuisce che, affinché sussista similitudine tra vero e modello, dovranno sussistere la similitudine geometrica, della distribuzione delle masse, delle forze ecc.
in cui i singoli termini
Dividendo l'espressione nelle variabili adimensionate
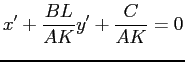
I termini
La condizione necessaria affinché modello e vero siano in similitudine è che siano uguali i gruppi adimensionali indipendenti meno uno.