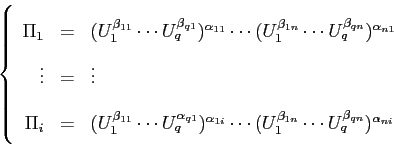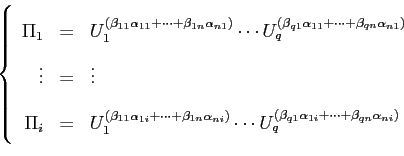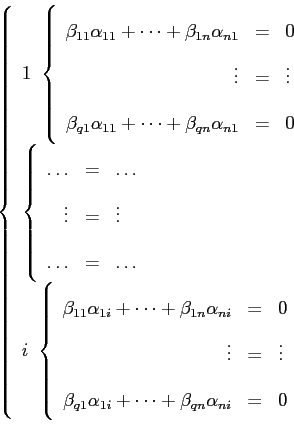Il teorema $\pi$ di Buckingam

Teorema D.1.1   Il numero di guppi adimensionali indipendenti è pari al numero dei parametri influenti meno il numero delle grandezze fondamentali.

$$i=n-q$$ (D.1)

(i)

$i$ numero dei gruppi adimensionali indipendenti;

(ii)

$n$ numero delle grandezze fondamentali;

(iii)

$q$ numero delle grandezze fondamentali che compaiono nel problema ($q=1$ problema geometrico $[l]$ , $q=2$ problema cinematico $[l, t]$ , $q=3$ problema dinamico $[l, m, t]$ ecc.).

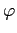
Dimostrazione. Sia $\varphi$ l'espressione matematica della grandezza della quale si vogliono ricavare i valori numerici tramite lo studio del modello in similitudine:

$$\varphi(x_1, \dots, x_n)=0$$

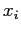
in cui $x_i$ sono i parametri influenti sul sistema. Procedendo all'adimensionalizzazione dell'espressione sopra si otterrà :

$$\varphi'(\Pi_1, \dots, \Pi_i)=0$$

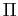
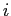
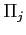
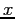
in cui $\Pi$ sono gli ``$i$ '' gruppi adimensionali indipendenti. Il generico elemento $\Pi_j$ sarà stato ottenuto a partire da un prodotto delle grandezze $x$ ciascuna elevata ad una data potenza per cui in generale si potrà dire:

$$\Pi_j=(x_1^{\alpha_{1j}} \cdots x_n^{\alpha_{nj}})$$

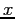
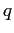
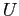
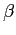
Le grandezze $x$ a loro volta potranno essere espresse come prodotto delle $q$ grandezze fondamentali $U$ del problema elevate alle potenze $\beta$ note:

$$x_j=U_1^{\beta_{1j}} \cdots U_q^{\beta_{qj}}$$

Si potrà allora scrivere:

$$\left\{ \begin{array}{rcl} \Pi_1&=&(U_1^{\beta_{11}} \cdots ... ...1n}} \cdots U_q^{\beta_{qn}})^{\alpha_{ni}} \end{array}\right.$$

$$\left\{ \begin{array}{rcl} \Pi_1&=&U_1^{(\beta_{11}\alpha_{1... ...}\alpha_{1i}+\cdots+\beta_{qn}\alpha_{ni})} \end{array}\right.$$

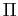
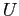
Poiché tutti i gruppi $\Pi$ sono adimensionali, tutti gli esponenti delle grandezze fondamentali $U$ dovranno essere nulli:

$$\left\{ \begin{array}{l} 1 \ \left\{ \begin{array}{rcl} \bet... ...beta_{qn}\alpha_{ni}&=&0 \end{array}\right. \end{array}\right.$$

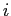
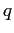
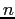
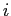
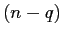
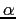
Si ottengono $i$ sistemi lineari omogenei ciasuno costituito da $q$ equazioni in $n$ incognite. Si deduce quindi che per la soluzione dovranno essere fissati per ciascuno degli $i$ sistemi $(n-q)$ valori di $\alpha$ . Dovendo essere tali (n-q)-ple indipendenti, esse dovranno essere proprio $i$ :

$$i=n-q$$

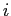
Risulta pertanto dimostrata la D.1. $\qedsymbol$