|
[linearc=0.5,cornersize=absolute,framesep=10pt]shadowcolor=black!70,blur=true ![\begin{psmatrix}[rowsep=1cm,colsep=1cm]
\psovalbox[fillstyle=solid,fillcolor=ye...
...e}{Calcolo}}
\ncline{->}{4,1}{5,1}%>{\textcolor{blue}{Calcolo}}
\end{psmatrix}](img540.png)
|
|
[linearc=0.5,cornersize=absolute,framesep=10pt]shadowcolor=black!70,blur=true ![\begin{psmatrix}[rowsep=1cm,colsep=1cm]
\psovalbox[fillstyle=solid,fillcolor=ye...
...e}{Calcolo}}
\ncline{->}{4,1}{5,1}%>{\textcolor{blue}{Calcolo}}
\end{psmatrix}](img540.png)
|
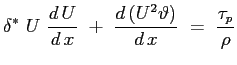
la
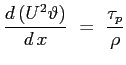
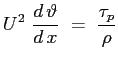
Si vede come della variazione di quantità di moto del flusso sia responsabile la sola
Si scelga a questo punto un profilo ipotetico di velocità , per esempio lineare, per la ![]() :
:
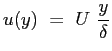
e si ipotizzi un atto di moto laminare, che permette l'utilizzo della espressione di Newton della viscosità :
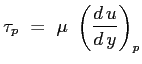
Con queste scelte si ottiene lo spessore di quantità di moto:
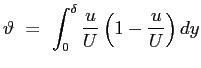
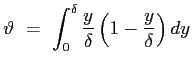
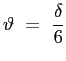
lo spessore di spostamento:
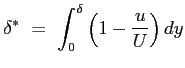
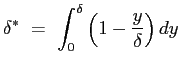
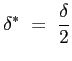
e lo sforzo a parete:
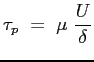
Si può calcolare lo spessore di strato limite
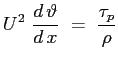
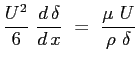
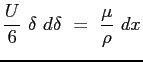
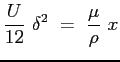
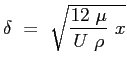
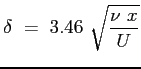
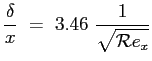
Lo sforzo tangenziale a parete locale sarà dunque:
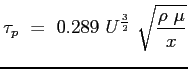
lo spessore di spostamento:
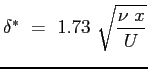
lo spessore di quantità di moto:
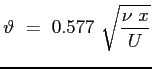
ed il coefficiente di resistenza della piastra di lunghezza
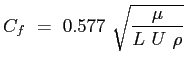
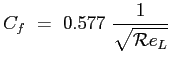
|