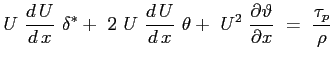Next: Spessore di spostamento Displacement
Up: Equazioni di Prandtl e
Previous: Considerazioni
Indice
le equazioni di Prandtl opportunamente integrate permettono di ottenere quella che si chiama equazione di Von Kàrmàn dello strato limite. Questa equazione permette di ottenere delle soluzioni dell'atto di moto nello strato limite nei casi di geometrie non semplici quali la lastra piana, a prescindere dalla natura laminare o turbolenta del moto in cui l'integrazione delle equazioni originarie risulta impossibile. L'equazione di Von Kàrmàn può essere ottenuta dalla elaborazione delle equazioni di Prandtl, oppure scrivendo il bilancio della quantità di moto in un volume di controllo che si estende lungo lo spessore dello strato limite6.2: da qui l'espressione ``integrale''.
La prima equazione, ossia quella di continuità delle Eq. (6.2) integrata considerando una distanza 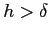 costante dalla superficie fornisce:
costante dalla superficie fornisce:
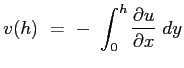 |
(6.3) |
Questa relazione mostra come la presenza di una 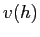 sia dovuta alla variazione della
sia dovuta alla variazione della 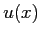 durante il moto affinché la portata rimanga immutata attraverso il volume di controllo.
durante il moto affinché la portata rimanga immutata attraverso il volume di controllo.
Integrata fino all'estremo 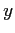 fornisce invece l'andamento della velocità
fornisce invece l'andamento della velocità 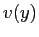 :
:
Si consideri ora la seconda delle Eq. (6.2):
e si sostituisca l'espressione del gradiente di pressione imposto dal campo esterno:
il terzo termine può essere sviluppato tenendo conto del risultato ottenuto dalla equazione di continuità :
mentre il secondo membro:
Sostituendo:
Essendo le funzioni integrali sicuramente convergenti l'operazione di derivazione parziale può essere portata fuori dal segno di operazione di integrale6.3:
Definendo:
l'equazione assume la sua forma:
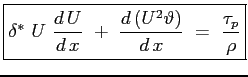 |
(6.4) |
Subsections




Next: Spessore di spostamento Displacement
Up: Equazioni di Prandtl e
Previous: Considerazioni
Indice
2009-01-26
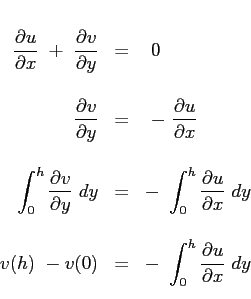
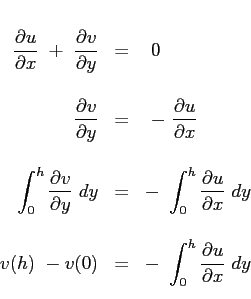
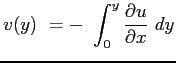
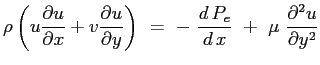
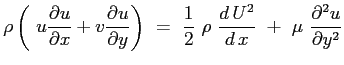
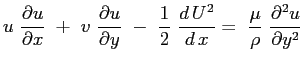
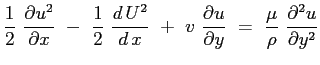
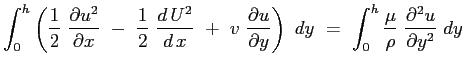
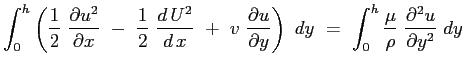
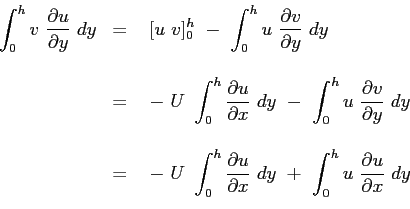
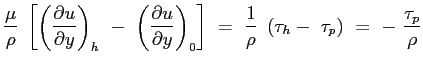
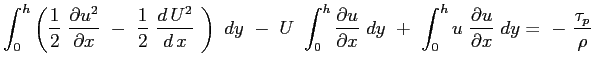
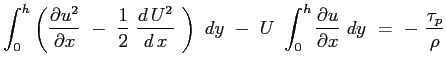
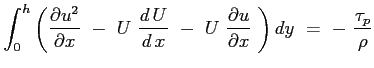
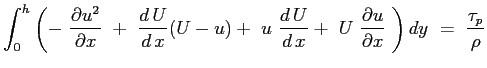
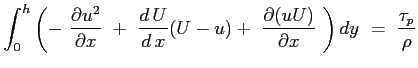
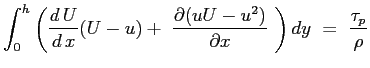
![$\displaystyle \int_0^h{ \left( \ensuremath{\frac{d\,U}{d\,x}}(U-u) +\ \ensuremath{\frac{\partial [u( U-u)]}{\partial x}}\ \right) dy} \ =\ \frac{\tau_p}{\rho}
$](img511.png)
![$\displaystyle \ensuremath{\frac{d\,U}{d\,x}}\ \int_0^h{(U-u)\ dy}\ +\ \ensuremath{\frac{\partial }{\partial x}} \int_0^h{[u( U-u)] dy} \ =\ \frac{\tau_p}{\rho}
$](img512.png)
![$\displaystyle U\ \ensuremath{\frac{d\,U}{d\,x}}\ \int_0^h{\left(1-\frac{u}{U}\r...
...ac{u}{U}\left( 1-\frac{u}{U}\right)\right] dy}\right] \ =\ \frac{\tau_p}{\rho}
$](img513.png)
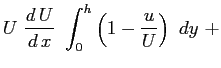
![$\displaystyle +\ 2\ U\ \ensuremath{\frac{\partial U}{\partial x}}\ \int_0^h{\le...
...\left[\frac{u}{U}\left( 1-\frac{u}{U}\right)\right] dy}\ =\ \frac{\tau_p}{\rho}$](img515.png)
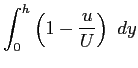
![$ \displaystyle \int_0^h{\left[\frac{u}{U}\left( 1-\frac{u}{U}\right)\right] dy}$](img520.png)