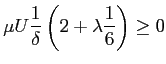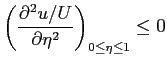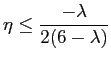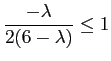Next: Parametri di strato limite
Up: Risoluzione integrale delle equazioni
Previous: Equazione di Von Kàrmàn: profilo
Indice
Il metodo di Polhausen è un metodo approssimato in quanto applicato all'equazione di Von Kàrmàn, che si basa sulle approssimazioni di Prandtl, e basato sull'adozione di un profilo di velocità ``a priori'' funzione della variabile adimensionata:
espresso dal polinomio:
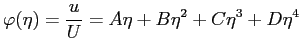 |
(6.6) |
che soddisfa già la condizione di aderenza a parete. Le condizioni al contorno sulla parete e al bordo di strato limite richieste al profilo di velocità sono:
c.c.
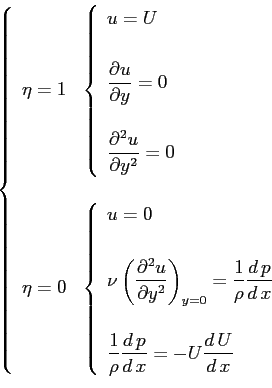
Le condizioni al contorno per 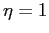 sono delle condizioni geometriche di ottimo raccordo con il campo esterno. Per
sono delle condizioni geometriche di ottimo raccordo con il campo esterno. Per 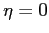 , la prima condizione rappresenta la condizione di aderenza, la seconda rappresenta l'equazione Eq. (6.2) di Von Kàrmàn a parete, la terza rappresenta la condizione di invarianza della pressione con
, la prima condizione rappresenta la condizione di aderenza, la seconda rappresenta l'equazione Eq. (6.2) di Von Kàrmàn a parete, la terza rappresenta la condizione di invarianza della pressione con 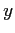 data dalla Eq. (6.1) di Bernouilli.
Al fine di soddisfare le condizioni al contorno date il polinomio dovrà essere necessariamente di quarto grado. Polhausen introduce il parametro adimensionato:
data dalla Eq. (6.1) di Bernouilli.
Al fine di soddisfare le condizioni al contorno date il polinomio dovrà essere necessariamente di quarto grado. Polhausen introduce il parametro adimensionato:
che tiene conto del campo esterno di velocità e del suo gradiente di pressione.
Derivando due volte la 6.6 si ottiene subito la costante 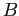 :
:
per 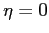 dalla seconda c.c. si ottiene:
dalla seconda c.c. si ottiene:
Scrivendo le condizioni al contorno per 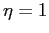 si ottiene un sistema di tre equazioni che permette di ottenere le costanti rimanenti
si ottiene un sistema di tre equazioni che permette di ottenere le costanti rimanenti 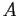 ,
, 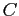 e
e 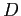 in funzione di
in funzione di 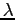 :
:
Risolto il sistema si ottiene:
L'espressione del profilo di velocità diventa:
che può anche essere scritta:
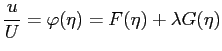 |
(6.7) |
Si possono calcolare i valori limite che 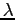 può assumere. Il minimo (quindi il massimo valore del gradiente di pressione positivo avverso) si trova imponendo l'annullamento della frizione a parete:
può assumere. Il minimo (quindi il massimo valore del gradiente di pressione positivo avverso) si trova imponendo l'annullamento della frizione a parete:
Figura 6.2:
Profilo di velocità di Polhausen.
|
|
Il valore massimo lo si cerca notando che le condizioni al contorno di raccordo, impongono che la derivata seconda del profilo di velocità debba essere negativa su tutto l'intervallo di variabilità di 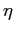 , per assicurare la concavità verso il basso:
, per assicurare la concavità verso il basso:
Si perviene alla disequazione di secondo grado:
Avendo già trovato il limite inferiore di 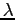 si studia il caso per
si studia il caso per 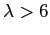 . Le soluzioni sono:
. Le soluzioni sono:
e:
Dovendo comunque risultare:
allora dovrà essere:
Subsections




Next: Parametri di strato limite
Up: Risoluzione integrale delle equazioni
Previous: Equazione di Von Kàrmàn: profilo
Indice
2009-01-26
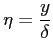
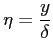
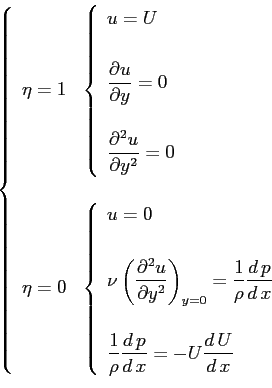
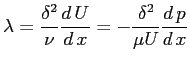
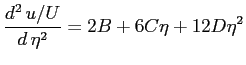
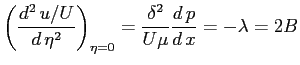
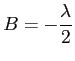
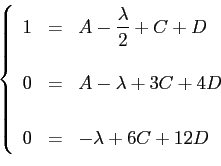
![\begin{displaymath}
\begin{array}{rcl}
A &=&\displaystyle 2 + \frac{\lambda}{6}\...
...\ [3pt]\\
D &=&\displaystyle 1 - \frac{\lambda}{6}
\end{array}\end{displaymath}](img592.png)
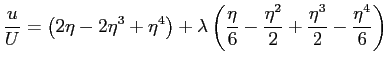
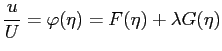
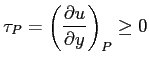
![$\displaystyle \mu U \frac{1}{\delta}\left[\left( 2 -6 \eta^2 + 4 \eta^3 + 4 \et...
...} - \eta + \frac{3}{2} \eta^2 -\frac{4}{6} \eta^3\right)\right]_{\eta=0} \geq0
$](img596.png)