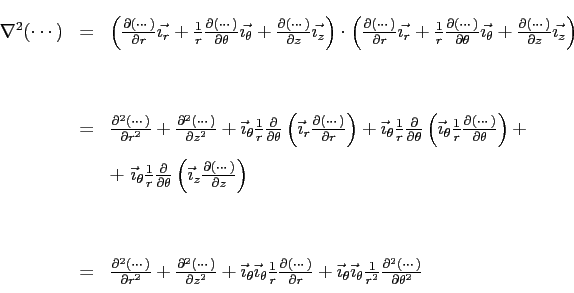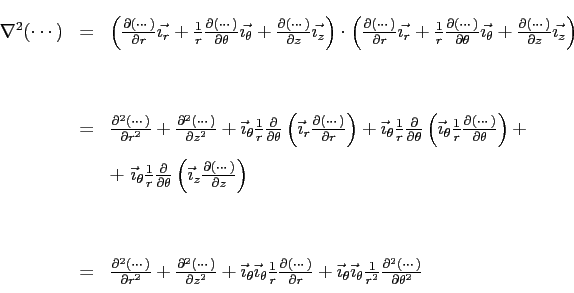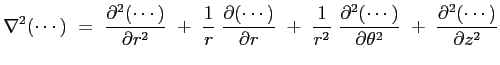Coordinate cilindriche

Nel ricavare l'espressione del laplaciano in coordinate cilindriche si deve fare qualche passaggio in più dovendo tener conto delle derivate dei versori.

$$\begin{array}{rcl} \nabla^2(\cdots) & = & \left(\ensuremath{... ...emath{\frac{\partial^2 (\cdots)}{\partial\theta^2}} \end{array}$$

$$\nabla^2(\cdots)\ =\ \ensuremath{\frac{\partial^2 (\cdots)}{\part... ...}{\partial\theta^2}}\ +\ \ensuremath{\frac{\partial^2 (\cdots)}{\partial z^2}}$$