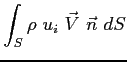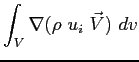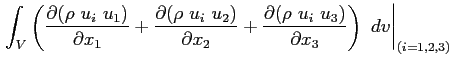Next: Risultante delle forze tangenziali
Up: Equazione di bilancio della
Previous: Equazione di bilancio della
Indice
L'equazione di bilancio della quantità di moto relativa ad un fluido confinato all'interno di un volume 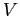 si ottiene ricorrendo alla seconda legge di Newton applicata a ciascuna delle particelle costituenti il fluido.
si ottiene ricorrendo alla seconda legge di Newton applicata a ciascuna delle particelle costituenti il fluido.
Considerando le forze agenti sulla particella fluida come:
- forze di volume
- forze di superficie
- forze di pressione
- forze tangenziali
l'espressione lagrangiana dell'equazione di bilancio integrale della quantità di moto assume la forma:
Applicando il teorema di Reynolds al primo membro dell'equazione sopra se ne ottiene la espressione integrale del bilancio della quantità di moto in forma euleriana:
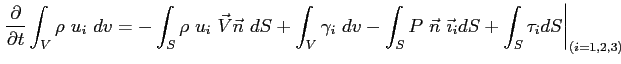 |
(2.2) |
Nell'espressione euleriana compare tra le forze presenti nel secondo membro il contributo dovuto alla quantità di moto del flusso di fluido scambiato dal volume di controllo attaverso la sua superficie con l'esterno2.2.
Sfruttando il teorema del flusso di Gauss, trasformando gli integrali di superficie che compaiono nella Eq. (2.2) in integrali di volume, si ottiene la forma differenziale della stessa, ossia le equazioni di Navier-Stokes.
Il flusso della quantità di moto diventa:
La risultante delle forze di pressione:
L'esplicitazione della risultante delle forze tangenziali richiede degli approfondimenti.




Next: Risultante delle forze tangenziali
Up: Equazione di bilancio della
Previous: Equazione di bilancio della
Indice
2009-01-26
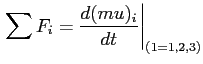
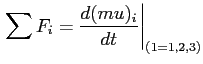
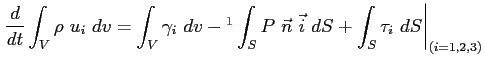
![\includegraphics[width=75mm]{qdm.eps}](img50.png)