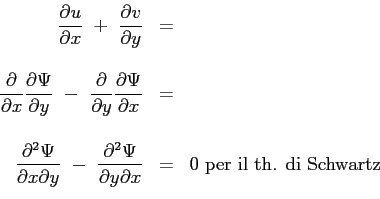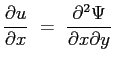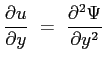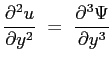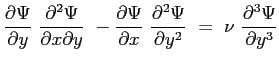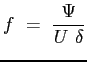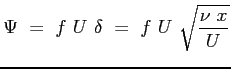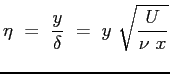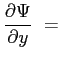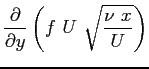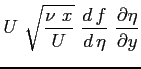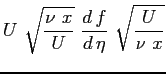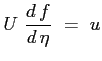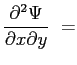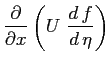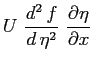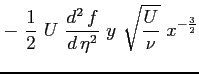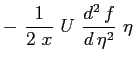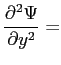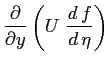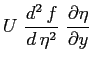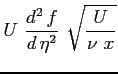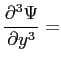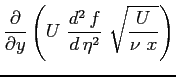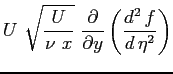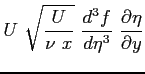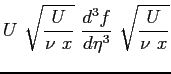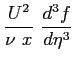Next: L'equazione di Blasius
Up: Equazione di Blasius: soluzione
Previous: Equazione di Blasius: soluzione
Indice
Figura 7.1:
Funzione di corrente
|
|
La funzione di corrente rappresenta la portata volumetrica che attraversa una linea qualunque che congiunge l'origine degli assi con il punto considerato.
Figura 7.2:
Portata elementare
|
|
da cui si ricavano 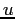 e
e 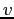 dividendo l'espressione sopra per
dividendo l'espressione sopra per 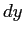 e
e 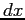 :
:
Si ricordano le ipotesi di lavoro:
- moto stazionario;
- moto bidimensionale;
- fluido incompressibile;
- semplificazioni di Prandtl;
- lastra piana, ossia
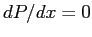 .
.
Le equazioni di Prandtl diventano:
con le condizioni al contorno:
c.c.
![\begin{displaymath}
\left\{
\begin{array}{rcl}
u(x,0)\ & = &\ 0 \\ [3pt]\\
v(x,0)\ & = &\ 0 \\ [3pt]\\
u(x,\infty)\ & = &\ U
\end{array}\right.
\end{displaymath}](img682.png)
La funzione di corrente soddisfa la prima equazione di continuità :
Nella seconda equazione della quantità di moto:
sostituendo si ottiene:
Ci si è ricondotti ad una equazione differenziale nella sola 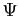 . A questo punto adimensionando ci si potrà ricondurre ad una equazione differenziale ordinaria in una sola variabile in virtù del fatto che le soluzioni sono profili affini.
. A questo punto adimensionando ci si potrà ricondurre ad una equazione differenziale ordinaria in una sola variabile in virtù del fatto che le soluzioni sono profili affini.
Si introducono la funzione di corrente adimensionata:
e la coordinata adimensionata 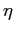 :
:
Si riportano tutti i calcoli per ottenere l'equazione definitiva di Blasius:




Next: L'equazione di Blasius
Up: Equazione di Blasius: soluzione
Previous: Equazione di Blasius: soluzione
Indice
2009-01-26
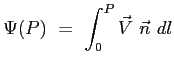
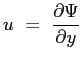
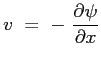
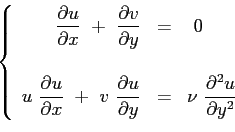
![\begin{displaymath}
\left\{
\begin{array}{rcl}
u(x,0)\ & = &\ 0 \\ [3pt]\\
v(x,0)\ & = &\ 0 \\ [3pt]\\
u(x,\infty)\ & = &\ U
\end{array}\right.
\end{displaymath}](img682.png)