![\begin{displaymath}
\begin{array}{rcl}\\ [3pt]
\displaystyle \rho \left(\ \ensur...
...ac{\partial w}{\partial z}}\ & = & \ 0 \\ [3pt] \\
\end{array}\end{displaymath}](img384.png)
![\begin{displaymath}
\begin{array}{rcl}\\ [3pt]
\displaystyle \rho \left(\ \ensur...
...ac{\partial w}{\partial z}}\ & = & \ 0 \\ [3pt] \\
\end{array}\end{displaymath}](img384.png)
vanno semplificate introducendo le seguenti ipotesi:
![\begin{displaymath}
\left\{
\begin{array}{rcl}
u&=&u(y,t) \\ [3pt]\\
v&=&0 \\ [3pt]\\
w&=&0 \\ [3pt]\\
p&=&P(y,t)
\end{array}\right.
\end{displaymath}](img385.png)
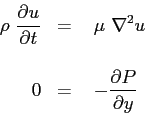
cioè :
![\begin{displaymath}
\left\{
\begin{array}{rcl}\\ [3pt]
\displaystyle \rho \ \ens...
...partial P}{\partial y}}\ & =&0 \\ [3pt] \\
\end{array}\right.
\end{displaymath}](img387.png)
Dalla seconda si deduce che il campo di pressione è ovunque costante e pari a quello del fluido in quiete. La prima equazione è quella che deve essere risolta con le condizioni iniziali:
|
Blue |
|
||||
|---|---|---|---|---|---|
|
Blue |
|
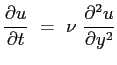
va risolta ricorrendo alla adimensionalizzazione delle variabili ed al teorema di Buckingam (vedi App.
Si vede che la relazione scritta sopra lega quattro grandezze:
ma a loro volta queste dipendono solo da due grandezze fondamentali:
lunghezza e tempo. In base al teorema di Buckingam l'equazione sopra può essere scritta in funzione di due gruppi adimensionali opportunamente scelti:
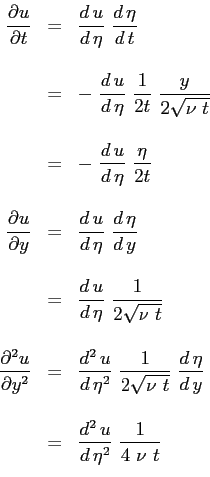
l'equazione diventa:
![\begin{displaymath}
\left\{
\begin{array}{rcl}
u(\eta=\infty) & = & 0 \\ [3pt]\\
u(\eta=0) & = & 1
\end{array}\right.
\end{displaymath}](img401.png)
Ci si è ricondotti anche in questo caso (Cf.ta Sez. 4.6) ad una equazione lineare ma omogenea. Le soluzioni fornite forniscono un profilo unico di velocità che si riproduce similmente a se stesso nel tempo. Infatti la
![\begin{displaymath}
\left\{
\begin{array}{rcl}
u'&=&y \\ [3pt]\\
y'\ +\ 2\ \eta\ y &=&0
\end{array}\right.
\end{displaymath}](img404.png)
Si cerca una funzione ausiliaria
Imponendo
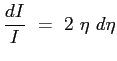
che risolta fornisce a meno di una costante:
quindi la
Sostituita nella equazione da risolvere:
Ricordando che
che integrata fornisce il profilo adimensionato cercato:
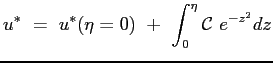
Tenendo conto delle condizioni al contorno per
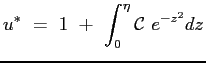
La costante
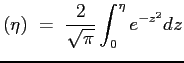
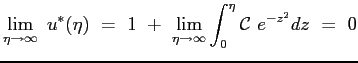
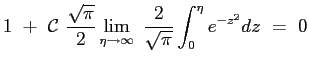
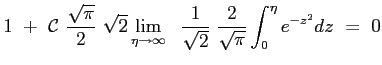
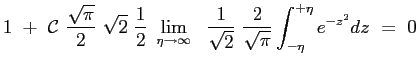
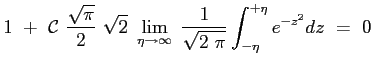
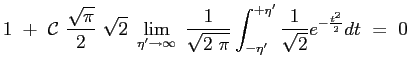
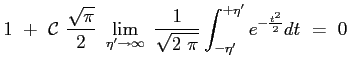
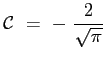
Si ottiene allora che il profilo della velocità adimensionata è dato proprio dalla funzione
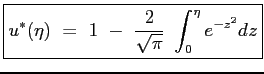 |
(5.3) |
Si può a questo punto calcolare lo spessore dello strato limite. Questo corrisponde per definizione alla distanza dal piano alla quale la velocità diventa pari al
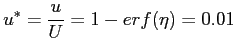
Dalla Tab.1045 di [2] si ricava che:
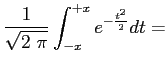 erf
erf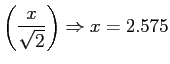
quindi:
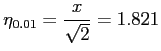
Lo spessore di strato limite si otterrà dalla:
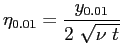
in cui si pone