



Next: Particolarizzazione delle equazioni di
Up: La viscosità
Previous: La viscosità
Indice
Il fenomeno della viscosità è un fenomeno di attrito. Esso nasce a causa del trascinamento che gli strati di fluido più veloci esercitano su quelli più lenti adiacenti o, viceversa, dall'azione frenante che gli strati più lenti esercitano su quelli più veloci adiacenti.
Questo effetto di trascinamento può essere immaginato come dovuto ad un trasferimento di quantità di moto tra strati a velocità differenti. Il meccanismo di trasferimento della quantità avviene a causa degli urti tra particelle degli strati a differenti velocità che per agitazione termica si trovano proiettate negli strati adiacenti.
Figura:
Meccanismo di trasferimento della quantità di moto
|
|
Il moto caotico di agitazione termica delle molecole determina la temperatura del fluido. L'energia di agitazione termica risulta distribuita equamente tra i gradi di libertà energetici2.11.
Tabella:
Gradi di libertà molecolari.
| width 3pt | RedN. atomi |
Redg.d.l. traslazionali |
Redg.d.l. rotazionali |
Redg.d.l. vibrazionali |
width 3pt |
| width 3pt |
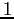
|
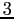
|
0
|
0
|
width 3pt |
| width 3pt |
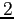 o lineari
o lineari |
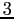
|
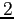
|
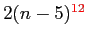 � �
|
width 3pt |
| width 3pt |
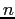
|
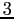
|
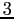
|
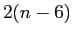
|
width 3pt |
|
L'energia cinetica di una molecola monoatomica è legata alla temperatura dalla relazione:
in cui:
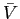 è la velocità media traslazionale di agitazione termica;
è la velocità media traslazionale di agitazione termica;
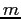 è la massa della molecola;
è la massa della molecola;
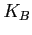 è la costante di Boltzman;
è la costante di Boltzman;
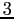 sono i gradi di libetà energetici di una molecola monoatomica;
sono i gradi di libetà energetici di una molecola monoatomica;
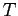 è la temperatura.
è la temperatura.
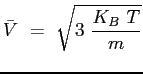 |
(2.18) |
Si può mostrare che la velocità media di agitazione termica sopra trovata è dello stesso ordine di grandezza della velocità di propagazione delle perturbazioni di pressione nel fluido (velocità del suono). Infatti:
in cui:
-
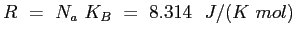 è la costante elastica dei gas perfetti;
è la costante elastica dei gas perfetti;
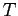 è la temperatura assoluta del gas;
è la temperatura assoluta del gas;
-
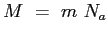 è la massa molare del gas;
è la massa molare del gas;
-
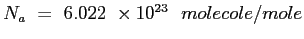 è il numero di Avogadro;
è il numero di Avogadro;
-
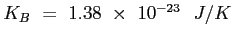 è la costante di Boltzmann;
è la costante di Boltzmann;
 è la massa molecolare del gas;
è la massa molecolare del gas;
-
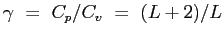
-
 calori specifici a pressione e volume costante;
calori specifici a pressione e volume costante;
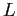 gradi di libertà energetici.
gradi di libertà energetici.
Queste due velocità sono quindi affini. Immettendo un disturbo di pressione in seno ad un fluido (e quindi una piccola quantità di energia), questo si propaga in virtù delle vibrazioni termiche delle molecole e gli urti che queste creano con le molecole adiacenti.
La distanza media percorsa da una molecola di gas tra due urti successivi viene dafinita libero cammino medio.
Durante il suo cammino la molecola, vista come una sfera di raggio 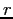 e massa
e massa 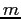 , urterebbe le altre molecole che si venissero a trovare all'interno di un volume cilindrico di raggio
, urterebbe le altre molecole che si venissero a trovare all'interno di un volume cilindrico di raggio 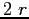 Il volume spazzato nell'unità di tempo sarebbe:
Il volume spazzato nell'unità di tempo sarebbe:
Se 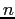 rappresenta il numero di molecole presenti nell'unità di volume allora il numero di urti nell'unità di tempo sarebbe:
rappresenta il numero di molecole presenti nell'unità di volume allora il numero di urti nell'unità di tempo sarebbe:
cui corrisponderebbe un tempo medio tra due urti successivi:
e quindi un libero cammino medio
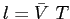 :
:
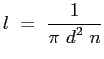 |
(2.19) |
Indicando con
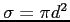 la sezione d'urto, le tre espressioni del libero cammino sono equivalenti:
la sezione d'urto, le tre espressioni del libero cammino sono equivalenti:
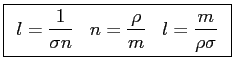 |
(2.20) |
Il libero cammino medio può essere interpretato anche come la distanza percorsa da una molecola che per agitazione termica passa da uno strato ad un altro di differente velocità prima di urtare un'altra particella (e subire a causa di questo urto una variazione della sua velocità ). Nel semplice caso monodimensionale 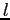 può essere visto come la variazione
può essere visto come la variazione
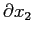 lungo la quale si concretizza la variazione
lungo la quale si concretizza la variazione
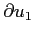 di velocità dovuta all'urto:
di velocità dovuta all'urto:
Se con 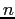 si è indicato il numero di molecole presenti nell'unità di volume allora:
si è indicato il numero di molecole presenti nell'unità di volume allora:
rappresenta il flusso di quantità di moto che attraversa la superficie elementare 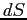 di separazione tra gli strati nell'unità di tempo. La forza di trascinamento scambiata tra gli strati attraverso la superficie
di separazione tra gli strati nell'unità di tempo. La forza di trascinamento scambiata tra gli strati attraverso la superficie 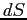 sarà allora:
sarà allora:
ne segue:
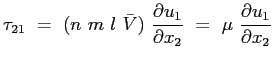 |
(2.21) |
Ricordando le Eq. (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) e Eq. (
) e Eq. (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
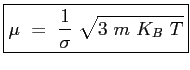 |
(2.22) |
Si vede che l'andamento teorico della viscosità è
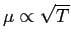 come da Fig.
come da Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
Figura:
Andamento teorico di 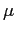 con
con 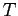 .
.
|
|
In effetti l'andamento reale differisce Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) da quello teorico alle basse temperature. La sezione d'urto infatti è influenzata dalla temperatura in quanto alle basse temperature si fanno sentire di più le forze repulsive che riducono l'entità degli urti. La sezione d'urto geometrica viene quindi corretta e opportunamente maggiorata. Si adotta a tale proposito la relazione di Sutherland:
da quello teorico alle basse temperature. La sezione d'urto infatti è influenzata dalla temperatura in quanto alle basse temperature si fanno sentire di più le forze repulsive che riducono l'entità degli urti. La sezione d'urto geometrica viene quindi corretta e opportunamente maggiorata. Si adotta a tale proposito la relazione di Sutherland:
Figura:
Andamento reale della viscosità .
|
|
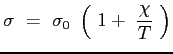 |
(2.23) |
La formula adottata per 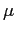 è allora quella di Sutherland:
è allora quella di Sutherland:
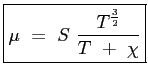 |
(2.24) |
in cui 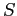 è la costante di Sutherland.
è la costante di Sutherland.
Tabella:
Costante di Sutherland per gas vari.
| width 3pt | RedGas |
RedS |
RedT |
width 3pt |
| width 3pt | Blue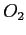
|
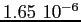
|
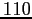
|
width 3pt |
| width 3pt | Blue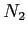
|
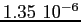
|
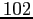
|
width 3pt |
| width 3pt | Blue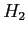
|
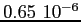
|
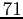
|
width 3pt |
| width 3pt | Blue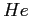
|
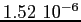
|
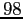
|
width 3pt |
| width 3pt | Blue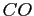
|
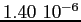
|
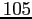
|
width 3pt |
| width 3pt | Blue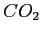
|
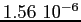
|
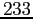
|
width 3pt |
| width 3pt | Blue
|
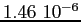
|
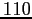
|
width 3pt |
|




Next: Particolarizzazione delle equazioni di
Up: La viscosità
Previous: La viscosità
Indice
2009-01-26
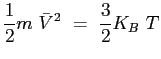
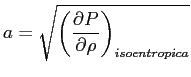
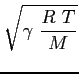
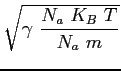
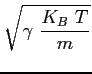
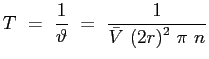
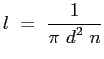
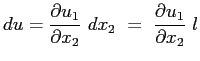
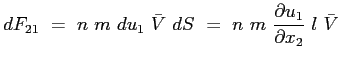
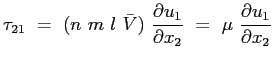
![]() da quello teorico alle basse temperature. La sezione d'urto infatti è influenzata dalla temperatura in quanto alle basse temperature si fanno sentire di più le forze repulsive che riducono l'entità degli urti. La sezione d'urto geometrica viene quindi corretta e opportunamente maggiorata. Si adotta a tale proposito la relazione di Sutherland:
da quello teorico alle basse temperature. La sezione d'urto infatti è influenzata dalla temperatura in quanto alle basse temperature si fanno sentire di più le forze repulsive che riducono l'entità degli urti. La sezione d'urto geometrica viene quindi corretta e opportunamente maggiorata. Si adotta a tale proposito la relazione di Sutherland:
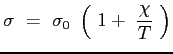
![]() è la costante di Sutherland.
è la costante di Sutherland.